whoway

# 面试模版part1

<font style="background:yellow">
<font style="background: MediumSpringGreen">
1
2

# 目录

[TOC]

# 1.排序算法的记忆『9+2』

学习排序算法的『原因』：获取排序算法中的『思想』

（1）插入类排序（3种）

  • 直接插入排序

  • 折半插入排序

  • 希尔排序

（2）选择类排序（2种）

  • 简单选择排序

  • 堆排序

    • 重点在于训练“堆”这种数据结构

（3）交换类排序（2种）

  • 冒泡排序

  • 快速排序

    • 训练“双指针”技巧、分治算法

（4）归并类（1种）

（5）**『不基于比较』**的排序算法类（1种）

  • 基数排序

以上为考研书籍中常写的9大排序算法。 就业面试中，不基于比较的排序算法类（3种）

基数排序、计数排序、桶排序

记忆：

  • 5大类排序算法，对应3+2+2+1+1
  • 9大考研基础排序算法+2大就业排序算法

# 1.1.时间复杂度『记』

# 1.1.1.平均时间复杂度

  • 1、军训的时候，教官说：快些以『O(nlogn)』的速度归队 （快速排序、希尔排序、归并排序、堆排序）
  • 2、特殊的比如：基数排序，平均时间复杂度『O(d(n+r))』
  • 3、9大排序中，others其他的没有列入的都是『O(n2)』

# 1.1.2.最坏时间复杂度

  • ✅平均⇔最坏
  • 9大排序中，除了快速排序是『O(n2)』之外
    • 其他的和平均时间复杂度一致

# 1.1.3.最好时间复杂度如下：

  • ✅平均⇔最好
  • 我觉得，冒泡之所以是n，或许是改进的版本，不然根本不能
    • 除了，冒泡和插入和平均有区别
    • 其他的和平均时间复杂度一致

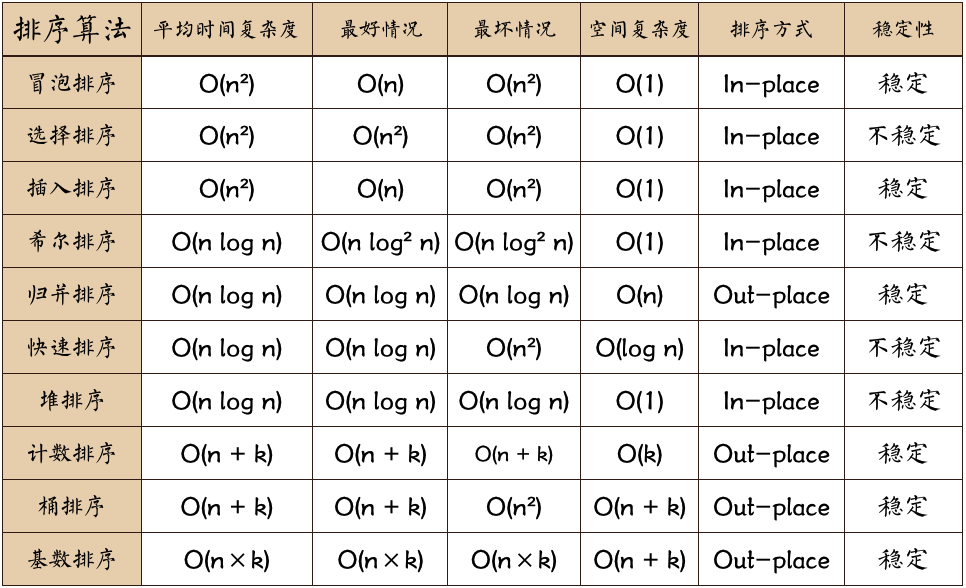
排序算法最好最坏

# 1.2.空间复杂度『记』

1.特殊的：

  • 快速排序为『O(logn)』——天勤上是『O(log2n)』

  • 归并排序为『O(n)』

  • 基数排序为『O(n+m)』

    2.9大排序中others（其他）的，都是『O(1)』

# 1.3.算法稳定性『记』

复习痛苦，情绪不稳定，快些选堆好友来聊天。
（快速排序、希尔排序、简单选择排序、堆排序）

其他的是稳定的。

注意点：关于“简单选择排序”
数组中的“交换版本”的为不稳定版本。
链表中的“插入版本”的为稳定版本。

  • 说到底就是，稳定不稳定，我们还是要看实现，但是如果没有具体说明算法执行流程，我们大致说：不稳定。

# 1.4.其他小提示『记』

  • 1、基于“比较”的排序，在最坏的情况下的时间复杂度至少是 『O(nlogn)』
  • 我以前还纠结到底是『O(nlogn)』还是『O(logn)』来着，后面大致给自己想了一个理解方式：
  • 『O(logn)』比『O(n)』增长慢，但是“基数排序”这样的不基于比较的算法才线性，那么我们基于比较的应该比他慢一些，时间要长一点。
  • 2、『『希尔排序时间复杂度很奇特。。』

# 1.5.外部排序

# 2.排序『数组』模板⭐️

# 2.0.排序数组版『面试代码框架』

  • 一定要记住三个函数！
 //1、播种随机数种子，如果不播种，也行，只是每次运行随机都是一样的。 
 srand(time(0));
 random_shuffle( arr.begin() , arr.end() );//arr是vector,2、面试用来生成随机数字序列 
 reverse( arr.begin(), arr.end() );//arr是vector
1
2
3
4
  • 模板开始
#include<bits/stdc++.h>
using namespace std;

//设置全局函数方便自己
vector<int> arr;
int len;


//——————————————————————某某排序模板放置位置——————————————————————
//选择排序
//void SelectSort(vector<int> &solve)
void SelectSort()
{
	for(int i=0; i<(len-1); ++i)
	{
		int preMin=i;
		for(int j=i+1; j<len; ++j)
		{
			if( arr[j]< arr[preMin] )
			{
				preMin=j;
			}
		}

		swap( arr[preMin], arr[i]);//调用函数，简化代码，也提高代码可读性
	}
}



//———————————————————————————————排序模板『vector数组版』——————————————————————————
void HelpSort( )
{
	//选择自己写的排序函数，比如我们选择『选择排序』
	SelectSort();//模板：函数名称
    
    //『如果面试官，看你现在写的是从大到小或者从小到大，让你改一下排序方向
    //那你就加上下面一行，来讲已经排序好的反转一下『后续的排序代码中，只管自己怎么高兴怎么写
    //不考虑从大到小，还是从小到大『尽量从小到大』
    reverse( arr.begin(), arr.end() );
	return ;
}


int main()
{
	//1、播种随机数种子，如果不播种，也行，只是每次运行随机都是一样的。 
	srand(time(0));

	scanf("%d",&len );
	arr.resize( len );	

	for(int i=0; i<len; ++i)
	{
		arr[i]=i;
	}
	//2、面试用来生成随机数字序列 
	random_shuffle( arr.begin() , arr.end() );

	HelpSort();//辅助排序函数
	for(int i=0; i<len; ++i)
	{
		printf("%d ",arr[i] );
	}

	return 0;
}
//———————————————————————————————排序模板『vector数组版』——————————————————————————
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

# 2.1.选择排序（SelectSort）

//设置全局函数方便自己
vector<int> arr;
int len;

//选择排序
void SelectSort()
{
	for(int i=0; i<(len-1); ++i)
	{
		int CurMin=i;
		for(int j=i+1; j<len; ++j)
		{
			if( arr[j]< arr[CurMin] )
			{
				CurMin=j;
			}
		}

		swap( arr[CurMin], arr[i]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 2.2.冒泡排序（BubbleSort）

  • 从小到大

  • 编程技巧：『逆向思维，倒着遍历』

# 2.2.1.未优化版

//冒泡排序——我们用『逆向思维，倒着遍历』
void BubbleSort()
{
	//逆向思维loop，倒着遍历
	for(int loop=len-1; loop>0; --loop)
	{
		for(int j=0; j<loop; ++j)
		{
			if( arr[j]>arr[j+1] ) 
			{
				swap(arr[j], arr[j+1]);
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 2.2.2.优化版

  • 增加一个辅助变量『空间换时间』
//冒泡排序——我们用『逆向思维，倒着遍历』
void BubbleSort()
{
	//逆向思维
	for(int loop=len-1; loop>0; --loop)
	{
		//辅助变量
		bool tag=true;
		for(int j=0; j<loop; ++j)
		{
			if( arr[j]>arr[j+1] ) 
			{
				swap(arr[j], arr[j+1]);
				//如果有调换位置，说明无序
				tag=false;
			}
		}

		//辅助变量没有变化，那肯定有序了，管你多少循环，我才懒得继续了
		if( tag )
		{
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 2.3.插入排序（InsertSort）

  • 从小到大

  • 编码技巧：『逆向思维，倒着遍历』

void InsertSort()
{
	//第1个元素，局部有序，所以我们从第2个元素，也就是1号开始
	for(int loop=1; loop<len; ++loop)
	{
        //『坑点』：记得，一定要弄好下标
		int CurNum=loop;
        
		//逆向思维
		for(int inner=loop-1; inner>=0; --inner)
		{
			if( arr[CurNum]<arr[inner] )
			{
				swap( arr[CurNum], arr[inner] );
                 //『坑点』记得更新下标
				CurNum=inner;
			} 
			else
			{
				break;
			}
		}//end for内部循环
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
  • 写法2，参见CyC2018『上述应该已经够清晰了』
void InsertSort(vector<int> & arr, int len)
{  
   //因为第0号元素默认有序，所以从i=1开始
   for(int i=1; i<len; ++i)
   {
       //待插入元素
       int num=arr[i];
       
       //从后往前面扫描
       int loop=i-1;
       while( loop>=0 && num<arr[loop] )
       {
           //右移
           arr[loop+1]=arr[loop];
           --loop;
       }

       arr[loop+1]=num;
   }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 2.4.希尔排序（Shell Sort）

  • 从小到大
  • 希尔排序，其实是对『插入排序』的改进
void ShellSort( vector<int>  & solve )
{
	int Len=solve.size();

    //获得希尔排序的增量，最接近Len的一个。。
	int h=1;
	while( h< Len/3 )
	{
		h=3*h+1;
	}
	
	while (h >= 1) 
	{
		for (int i = h; i < Len; ++i) 
		{
            //从后往前遍历『j>=h && solve[j]<solve[j-h]』
			for (int j = i; j >= h && solve[j]<solve[j-h] ; j -= h) 
			{
				swap( solve[j], solve[j-h] );
			}
		}
        
        //逐步缩小增量的大小
		h = h / 3;
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
  • 参考自：CyC2018
void shellSort( vector<int> & arr )
{
	//希尔排序的增量
	int d=arr.size();
	while( d>1 )
	{
		//使用希尔增量的方式，即每次折半
		d=d/2;
		for(int loop=0; loop<d; ++loop)
		{
			for(int i=loop+d; i<arr.size(); i+=d )
			{
				int temp=arr[i];
				int j;
				for( j=i-d; j>=0 && arr[j]>temp; j=j-d )
				{
					arr[j+d]=arr[j];
				}
				arr[j+d]=temp;
			}
		}
	}	
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 2.5.堆排序（HeapSort）

从小到大

思想：局部治理，问题一步步变小，减而治之

#include<bits/stdc++.h>
using namespace std;

vector<int> solve;
//辅助函数1
void up2downSink(int upPos, int downPos)
{
	int needModify=upPos;
	int LChild=needModify*2;

	while( LChild<=downPos )
	{
		int RChild=LChild+1;
		if( RChild<=downPos && solve[RChild]>solve[LChild] )
		{
			LChild=RChild;
		}

		if( solve[LChild]>solve[needModify] )
		{
			swap( solve[LChild], solve[needModify] );
			needModify=LChild;
			LChild=needModify*2;
		}
		else
		{
			break;
		}
		
	}
}



//辅助函数2
//创建大顶堆【begin,end】
void createMaxHeap(int begin, int end )
{
	for(int loop=(end/2); loop>=begin; --loop )
	{
		up2downSink(loop, end);
	}
}


//核心代码【begin,end】
void heapSort(int begin, int end)
{
	if( begin>=end ) return ;
	
	createMaxHeap( begin, end );
	for(int loop=end; loop>begin; --loop)
	{
		//将大顶堆的最大值solve[begin]和当前最后的元素换位置
		swap( solve[loop], solve[begin] );
		//将插入的元素，进行下沉，到我们不能管的边界loop-1
		//因为我们认为，loop已经可以了
		up2downSink(begin, loop-1);
	}
}


int main()
{
	int n;
	while( ~scanf("%d",&n) )
	{
		solve.resize(n);
		for(int i=0; i<n; ++i)
		{
			scanf("%d",&solve[i]);
		}
		heapSort(0,n-1);

		for(int i=0; i<n; ++i)
		{
			printf("%d%c",solve[i], i!=(n-1) ? ' ' : '\n' );
		}
	}


	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

# ✅可以分成2个函数

# 2.6.归并排序(也可1个函数⭐️)

# 1核心函数⭐️

void mergesort( vector<int> &arr, int left, int right){
    if( left<right ){
        int mid=left+(right-left)/2;
        mergesort( arr, left, mid);
        mergesort( arr, mid+1, right);

        vector<int> help=arr; //就是这里花费了空间，但是建议这里修改！
      
        int indexLeft=left, indexRight=mid+1;
        int cur_fill_index=left;
        while( indexLeft<=mid && indexRight<=right ){
            if( help[indexLeft]<=help[indexRight] ){
                arr[cur_fill_index++]=help[indexLeft++];
            }
            else{
                arr[cur_fill_index++]=help[indexRight++];
            }
        }

        while( indexLeft<=mid ){
            arr[cur_fill_index++]=help[indexLeft++];
        }
        while( indexRight<=right ){
            arr[cur_fill_index++]=help[indexRight++];
        }
    }

    return ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
  • 修改后
void mergesort( vector<int> &arr, int left, int right){
    if( left<right ){
        int mid=left+(right-left)/2;
        mergesort( arr, left, mid);  //递归分治，划分
        mergesort( arr, mid+1, right);//递归分治，划分

      	//就是这里花费了空间
        vector<int> help;
        for(int i=left; i<=right; ++i){
            help.push_back(arr[i]);
        }
        int offset=left;
        //=============
      //或者改为下面这样！易错点是：help必须指定大小，如果不指定，使用copy函数会报错！⭐️
      /*
      	vector<int> help(right-left+1);//就是这里花费了空间
        copy( arr.begin()+left , arr.begin()+right+1, help.begin() );
      */
        int indexLeft=left, indexRight=mid+1;
        int cur_fill_index=left;
        while( indexLeft<=mid && indexRight<=right ){
            if( help[indexLeft-offset]<=help[indexRight-offset] ){
                arr[cur_fill_index++]=help[indexLeft-offset];
                ++indexLeft;
            }
            else{
                arr[cur_fill_index++]=help[indexRight-offset];
                ++indexRight;
                //增加地方
                res+=(mid-indexLeft+1);
            }
        }

        while( indexLeft<=mid ){
            arr[cur_fill_index++]=help[indexLeft-offset];
            ++indexLeft;
        }
        while( indexRight<=right ){
            arr[cur_fill_index++]=help[indexRight-offset];
            ++indexRight;
        }
    }

    return ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

# 开拓思维的子函数1

88. 合并两个有序数组 (opens new window)

  • 技巧——倒着来
class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        
        int one=m-1;
        int two=n-1;
        int tag=m+n-1;
        while( one>=0 && two>=0 )
        {
            if( nums1[one]>nums2[two] )
            {
                nums1[tag--]=nums1[one--];
            }
            else
            {
                nums1[tag--]=nums2[two--];
            }
        }

        if( one<0 )
        {
            while( two>=0 && tag>=0 )
            {
                nums1[tag--]=nums2[two--];
            }
        }

        if( two<0 )
        {
            while( one>=0 && tag>=0 )
            {
                nums1[tag--]=nums1[one--];
            }
        }

        return ;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# ⭐️关于「逆序对」借助“归并排序”⭐️

class Solution {
public:
    int reversePairs(vector<int>& nums) {
        vector<int> tmp(nums.size());
        return mergeSort(0, nums.size() - 1, nums, tmp);
        
    }
private:
    int mergeSort(int l, int r, vector<int>& nums, vector<int>& tmp) {
        // 终止条件
        if (l >= r) return 0;
        // 递归划分
        int m = (l + r) / 2;
        int res = mergeSort(l, m, nums, tmp) + mergeSort(m + 1, r, nums, tmp);
        // 合并阶段
        int i = l, j = m + 1;
        for (int k = l; k <= r; k++)
        {
            tmp[k] = nums[k];
        }


        for (int k = l; k <= r; k++) {
            if (i == m + 1) //左边区间已经合并完，只需合并右边区间
            {
                nums[k] = tmp[j++];
            }
            else if (j == r + 1 || tmp[i] <= tmp[j])//左边区间的元素比右边小，不用计算逆序对
            {
                nums[k] = tmp[i++];
            }
            else {
                nums[k] = tmp[j++];
                res += m - i + 1; // 统计逆序对
            }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# 我的模版

int res=0;

void mergesort( vector<int> &arr, int left, int right){
    if( left<right ){
        int mid=left+(right-left)/2;
        mergesort( arr, left, mid);
        mergesort( arr, mid+1, right);

        vector<int> help;//就是这里花费了空间
        for(int i=left; i<=right; ++i){
            help.push_back(arr[i]);
        }
        int offset=left;
      
        int indexLeft=left, indexRight=mid+1;
        int cur_fill_index=left;
        while( indexLeft<=mid && indexRight<=right ){
            if( help[indexLeft-offset]<=help[indexRight-offset] ){
                arr[cur_fill_index++]=help[indexLeft-offset];
                ++indexLeft;
            }
            else{
                arr[cur_fill_index++]=help[indexRight-offset];
                ++indexRight;
                //增加地方
                res+=(mid-indexLeft+1);
            }
        }

        while( indexLeft<=mid ){
            arr[cur_fill_index++]=help[indexLeft-offset];
            ++indexLeft;
        }
        while( indexRight<=right ){
            arr[cur_fill_index++]=help[indexRight-offset];
            ++indexRight;
        }
    }

    return ;
}

class Solution {
public:
    
    int reversePairs(vector<int>& nums) {
        res=0;
        mergesort( nums, 0, nums.size()-1); //借助sort函数
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

# 2.7.快速排序(也可1个函数⭐️)「图解」

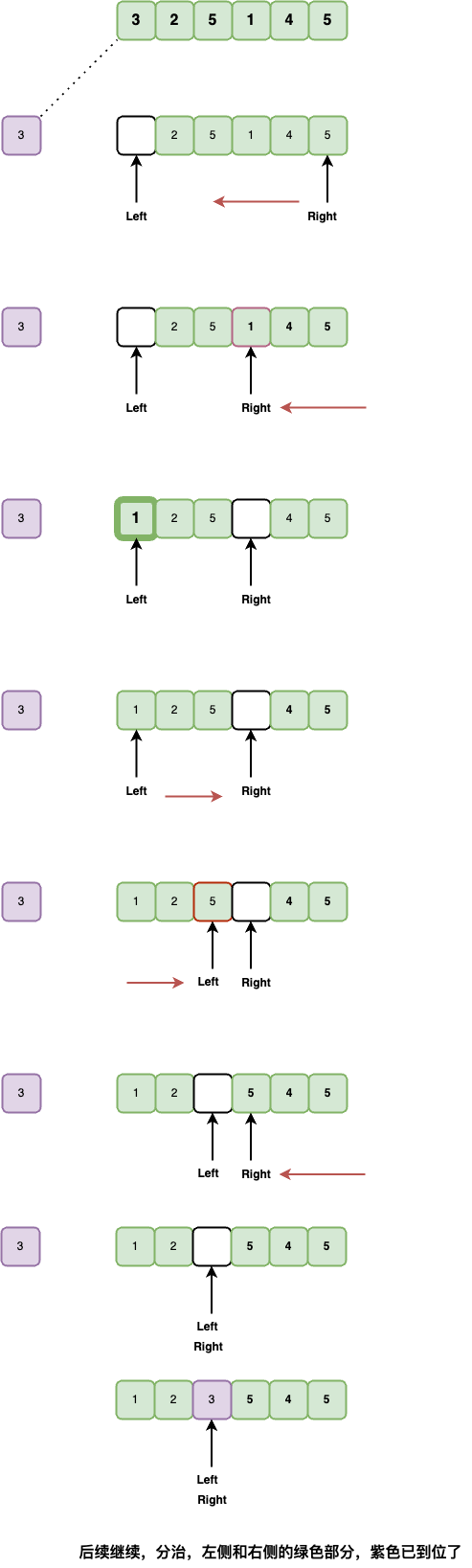
# 2.7.1.一般版本

  • 下面，用全集和补集的方式进行了展示记忆方法。
  • 快速排序的不稳定性来源：知乎 (opens new window)

# 2.7.2.合并2函数为1函数

  • 递归的写法！
//注意，是『闭区间』【Left，Right】
void QuickSort( int Left, int Right )
{
	if( Left<Right )
	{
		//模拟参数传递
		int start=Left;
		int end=Right;

    //假装，选最左边的元素作为坑
		int SelectElement=arr[start];
		while( start<end )
		{
      
			while( start<end && arr[end]>SelectElement )
			{
				--end;
			}
			arr[start]=arr[end];
      
      //『『坑点』』2：arr[start]<=SelectElement取的是<=
        //可以这么理解，arr[下标]和SelectElement的关系只有>和<和==，我们采用的是补集
        //此外，从算法的书籍中介绍到，我们不仅仅可以用本代码中这种方式，>和<=，我们还可以用>=和<
        //此外，这个判断==并不是快速排序的不稳定性来源！！！
			while( start<end && arr[start]<=SelectElement )
			{
				++start;
			}
			arr[end]=arr[start];
      
		}

		//一定要记得把坑，填好
		arr[end]=SelectElement;
		int PosHole=start;

		QuickSort( Left, PosHole-1 ); //分治左边
		QuickSort( PosHole+1, Right );//分治右边
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
1、作为最常用**的算法之一，最好能在一分钟内写出来，生活、工作、面试必备良品。
2、思路：其实选择一个数字枢轴作为枢纽pivot，左右指针向中间靠拢，将大于pivot的都置换到其右面，小于pivot的都置换到其左边。然后左递归，右递归，类似二叉树的先序遍历。
3、注意：下面的程序选择最左的数作为pivot，当然还可以随机选，选择哪个数也是比较有研究的，请查阅相关资料。
1
2
3

# 3.排序『链表』模板⭐️

# 3.1.选择排序

# 3.1.1不断链之狸猫换太子版『修改节点』

  • 牛客和LeetCode上都会超时，但思路OK
/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

void swap( ListNode * a, ListNode * b)
{
    int temp=a->val;
    a->val=b->val;
    b->val=temp;
    
    //a->val^=b->val;  //由于『优先级』，这样写是错误的，要写成 (a->val)^=(b->val)这样的
    //b->val^=a->val;
    //a->val^=b->val;
}

class Solution {
public:
    /**
     * 
     * @param head ListNode类 the head node
     * @return ListNode类
     */
    ListNode* sortInList(ListNode* head) {
        // write code here
        
        
        //****************************************************************************
        ListNode * cur=head;
        
        while( nullptr!=cur )
        {
            ListNode * mintemp=cur;
            ListNode * inner=cur;
            
            while( nullptr!=inner )
            {
                if( inner->val < mintemp->val )
                {
                    mintemp=inner;
                }
                
                inner=inner->next;//for inner loop
            }
            swap( mintemp, cur );//简化代码
            
            cur=cur->next;//for outside loop
        }
        //****************************************************************************
        
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

# 3.1.2.断链写法『不修改节点』

# 3.3.插入排序

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if( nullptr==head || nullptr==head->next )
        {
            return head;
        }

        ListNode * sentry=new ListNode(0); //表示
        ListNode * cur=head;                  //表示，要排序的一串节点中最开始的节点
        //第1个大于等于Cur的节点
        ListNode * FirstGTECur=sentry;            //前面的节点中，排序完成的最后一个节点
       

        while( nullptr!=cur )
        {
            //找到一个比当前节点还大的节点，方便插入
            while( nullptr!=FirstGTECur->next && FirstGTECur->next->val < cur->val )
            {
                FirstGTECur=FirstGTECur->next;
            }

            //链表的拆解和链接
            ListNode * CurTempNext=cur->next;
            cur->next=FirstGTECur->next;    //链表的
            FirstGTECur->next=cur;

            FirstGTECur=sentry;//重新回到原点，重新开始下一轮『核心』
            cur=CurTempNext;   
        }

        return sentry->next;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# ✅『2大』

# 3.6.归并排序

# 1.子函数1

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        
        if(nullptr==l1)
        {
            return l2;
        }

        if(nullptr==l2)
        {
            return l1;
        }

        ListNode * rt;
        if(l1->val < l2->val)
        {
            rt=l1;
            l1=l1->next;
        }
        else
        {
            rt=l2;
            l2=l2->next;
        }

        //当前指针
        ListNode * p=rt;

        while(nullptr!=l1 && nullptr!=l2)
        {
            if(l1->val < l2->val)
            {
                p->next=l1;
                p=p->next;

                l1=l1->next;
            }
            else
            {
                p->next=l2;
                p=p->next;
                
                l2=l2->next;
            }
        }

        if(nullptr==l1)
        {
            p->next=l2;
        }
        else
        {
            p->next=l1;
        }

        return rt;
    }
    
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
  • 下面是这个的递归版本
ListNode* mergeTwoLists(ListNode* L1, ListNode* L2) 
{
    if( nullptr==L1 )
    {
        return l2;
    }
    if( nullptr==L2 )
    {
        return L1;
    }
    
    
    //递归
    if( L1->val < L2->val )
    {
        L1->next=mergeTwoLists( L1->next, L2 );
        return L1;
    }
    else
    {
        L2->next=mergeTwoLists( L1 , L2->next );
        return L2;
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 3.7.快速排序


void swap( ListNode * a, ListNode *b)
{
    int temp=a->val;
    a->val=b->val;
    b->val=temp;
}

ListNode * Divide( ListNode * begin, ListNode * end )
{
    //不需要排序的特例
    if( nullptr==begin ||begin==end )
    {
        return begin;
    }

    int SelectKey=begin->val;

    //左侧一大块比SelectKey小的元素，最右边的边界位置
    //『此外，Left就是那个被挖出来的坑』
    ListNode * Left=begin;   
    ListNode * Right=begin->next;//右侧一大块>=SelectKey的元素，最左边的边界位置

    //想办法把<Key的元素换到前面去
    while( Right!=end )
    {
        if( Right->val < SelectKey )
        {
            //左侧让一个坑出来，准备和它换
            Left=Left->next;
            swap(Left,Right);
        }

        Right=Right->next;
    }

    //把先前选择的SelectKey这个元素填进坑里面
    swap(Left,begin);

    return Left;
}

void QuickSort( ListNode *  begin, ListNode * end )
{
    //不需要排序的特例
    if( nullptr==begin  || begin==end  )
    {
        return ;
    }

    ListNode * pos=Divide( begin, end );
    QuickSort( begin,pos );
    QuickSort( pos->next,end ); 
}
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        QuickSort(head,nullptr);
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

# 5.查找类算法

# 5.1.二分查找

# 5.1.1.自建轮子

  • 分while(L<R)和while(L<=R)这2种方式「核心难点」——理解
int mid= Left + (Right-Left)/2 
       = 2*Left/2 +(Right-Left)/2 
       = (Left+Right)/2
1
2
3

# 记忆口诀：LRL

# 5.1.2.STL解法

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        pair<vector<int>::iterator,vector<int>::iterator> solve;
        solve=equal_range(nums.begin(),nums.end(),target);

        int tag=0;
        for(int i: nums)
        {
            if( target==i )
            {
                tag=1;
                break;
            }
        }

        vector<int> ret;
        
        //那显然后面就更加没有了
        if( nums.end()==solve.first  )
        {
            ret.push_back(-1);
            ret.push_back(-1);
            return ret;
        }

        
        if( 1==tag )
        {
            
            ret.push_back( solve.first-nums.begin() );
            ret.push_back( solve.second-nums.begin()-1 );
            return ret;
        }
        else
        {
            ret.push_back(-1);
            ret.push_back(-1);
            return ret;
        }

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

# 5.2.其他查找算法

# 参考资料

# 1.并查集UnionSet『模板』

# 1.1.模板题

# 1.2.最终ADT模板设计✔️

  • 设计思想阐述：
  • 1.初始化，所有节点的父节点都是自己『表示，我是一座孤岛』
  • 2.merge，孤岛之间开始连接
    • 2.1.如果纯粹连接，发现会可能出现『闭环』
    • 2.2.为了解决闭环『我们需要设计一个函数』用于获得我们这块岛屿的岛主leader
//抽象数据类型（Abstract Data Type，ADT），也就是我们设计的『并查集』
class UnionSet
{
	//1、内置『封装』的数据结构
	private:
		int num;//不连通分量
		vector<int> parent;
	//2、算法
	public:
		bool connected(int a, int b);	//判断是否连通
		int count();					//『必要』返回几个集合、也就是：判断有多少个不连通图
		void merge(int first, int second);//『必要』合并集合
		int findFather(int x);		//『必要、必要性证明见后边』查找x在哪个集合，找最终父亲结构 
		UnionSet(int n):num(n)		//『必要』
		{ 
			parent.resize(n); 
		};
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 1.3.findFather函数存在的必要性证明：

class UnionSet
{
public:
    UnionSet(int n)
    {
        father.resize(n);
        for(int i=0; i<n; ++i)
        {
            father[i]=i;
        }
    }
    //出错的地方，就在于,merge的策略太简单，所以是不OK的
    /*
    [[1,1,1],[1,1,1],[1,1,1]]
    输出
    0	『错位』
    预期结果
    1
	*/
    void merge(int first, int second)
    {
        if( first>second )
        {
            swap(first,second);
        }

        if( father[first]==second ||father[second]==first )
        {
            return ;
        }

        if( father[first]!=first )
        {
            father[second]=first;
            return ;
        }
        else //if( father[second]!=second )
        {
            father[first]=second;

        }

    }
    int ret()
    {
        int res=0;
        for(int i=0; i<father.size(); ++i)
        {
            if( father[i]==i )
            {
                ++res;
                //cout<<"ok"<<i<<endl;
            }
        }
        return res;
    }
private:
    vector<int> father;
};


class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        
        int Len=isConnected.size();
        if( 0==Len )
        {
            return 0;
        }
        UnionSet solve( Len );
        for(int i=0; i<Len; ++i)
        {
            for(int j=0; j<i; ++j)
            {
                if( 1==isConnected[i][j] && i!=j )
                {
                    solve.merge(i,j);
                }
            }
        }

        return solve.ret();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
  • 改进之后
class UnionSet
{
public:
    UnionSet(int n)
    {
        father.resize(n);
        for(int i=0; i<n; ++i)
        {
            father[i]=i;
        }
    }
    //修改merge的策略，稍微好一点
    void merge(int first, int second)
    {
        int a=findFather( first );
        int b=findFather( second );
        if( a==b )
        {
            return ;
        }
        else
        {
            father[a]=b;
            return ;
        }
    }
    int ret()
    {
        int res=0;
        for(int i=0; i<father.size(); ++i)
        {
            if( father[i]==i )
            {
                ++res;
                //cout<<"ok"<<i<<endl;
            }
        }
        return res;
    }
private:
    vector<int> father;
    int findFather(int val)		//内部的辅助函数
    {
        while( val!=father[val] )
        {
            val=father[val];
        }
        return val;
    }
    
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

# 1.4.如何缩短findFather函数的搜索速度

  • 显然，我们在每次查询findFather之后进行一次重新Father(val)=XXX就行了
    • 我的想法是：只有findFather查询一次，我才优化一次『非必要不主动优化』
    • 注意：我的方法和主流的UnionSet优化方式是不同的！！

# 2.单调栈MonotonousStack『模板』

  • 参考：单调栈解题模板秒杀8个题 (opens new window)

  • mo-not-on-ous

  • 难点—不知道ADT

  • 单调栈实际上是栈，只是利用一些巧妙的逻辑：

  • 使得『每次』新元素入栈后，栈内的元素都保存单调！（单调递增或单调递减）

尝试创建：ADT

# 2.1.模板题

# 2.1.1.例1-最大的矩形

  • CCF.2013 12-3.最大的矩形（单调栈）

# 2.1.2.例2-下一个更大的元素

# 2.1.3.每日温度

# 2.2.最终ADT模板设计✔️

  • 这个栈满足一个性质：数列中的所有元素只会进出单调栈一次
  • 这个算法的过程用一句话总结就是，如果压栈之后仍然可以保持单调性，那么直接压。否则先弹出栈的元素，直到压入之后可以保持单调性。
  • 这个算法的原理用一句话总结就是，被弹出的元素都是大于当前元素的，并且由于栈是单调减的，因此在其之后小于其本身的最近的就是当前元素了
  • 单调栈在栈的基础上进一步受限，即要求栈中的元素始终保持单调性。
//我们设计，从栈底到top是『单调递增』的
class MonotonousStack
{
public:
	void push( int val );
    int top( );			//返回栈顶
    
    //push前调整栈的单调性『这个接口，本来不应该有的,但是很多单调栈的题目，很喜欢用这个二等公民』
    void beginPushAdjust( int val );	
private: 
    stack<int> data;
};
1
2
3
4
5
6
7
8
9
10
11
12
  • 实现如下
//我们设计，从栈底到top是『单调递增』的
class MonotonousStack
{
public:
	void push( int val );
    {
        beginPushAdjust(val);
        data.push(val);
    }
    int top( );			//返回栈顶
    {
        if( !data.empty() )
        {
            return data.top();
        }
        else
        {
            throw "error func call";
        }
    }
    void beginPushAdjust( int val ) //push前调整栈的单调性
    {
        while( ( !data.empty() ) && data.top()>val )
        {
        	data.pop();    
        }
    }
private:
    stack<int> data;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# 2.3.单调栈解题『坑』『模板』⭐️

  • 单调栈，用于解题，常常用的是『二等公民』
//伪代码如下
MonotonousStack solve;
for( 循环 )
{
    solve.beginPushAdjust( 值val );
    //获得solve.top();
    //利用写你的解题逻辑
    solve.push( 值val );
}
1
2
3
4
5
6
7
8
9

# 3.单调队列MonotonousQueue『模板』可设计ADT

ACM中的使用：

单调队列：单调队列即保持队列中的元素单调递增（或递减）的这样一个队列『可以从两头删除， 只能从队尾插入』

  • 这个队列满足一个性质：数列中的所有元素只会进出单调队列一次

# 3.1.模板题

# 3.1.1.例题-滑动最小值

  • 《挑战程序设计竞赛》

# 3.1.2.志愿者选拔

# 3.1.3.滑动窗口的最大值

# 3.2.最终ADT模板设计✔️

  • 从实际上还是队列，只是利用一些巧妙的逻辑：
  • 使得『每次』新元素入队列后，队列内的元素都保存单调！（单调递增或单调递减）
  • 这个队列满足一个性质：数列中的所有元素只会进出单调队列一次
  • 单调队列在添加(push)元素的时候靠删除元素保持队列的单调性，相当于抽取出某个函数中单调递增（或递减）的部分。
  • 设计的ADT的算法如下
    • 设计从front到尾巴『单调递减的队列』
    • 内部：借助双端队列实现
    • 记忆下面『3个』函数
class MonotonousQueue
{
public:
    //在队尾添加元素n，如果n比前面的元素大，则『压掉它』也就是去除
    void push(int n);	
    //返回当前队列中的队头『单调递减，所以正好是队头』
    int retFrontMax();
    //队头元素如果刚刚好是val，那么删掉它！
    void popIsVal(int val);
    
private:
    deque<int> data;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
  • //设计从front到尾巴『单调递增的队列』差不多同理
class MonotonousQueue
{
public:
    //在队尾添加元素val，如果n比前面的元素大，则『压掉它』也就是去除
    void push(int val);	
    {
        //如果是非空的，并且data的尾巴元素小于val
        while( (!data.empty()) && data.back()<val )
        {
			data.pop_back();
        }
        data.push_back( val );
    }
    //返回当前队列中的队头『单调递减，所以正好是队头』
    int retFrontMax();
    {
        if( 0==data.size() )
        {
            throw "error func call";
        }
        else
        {
            return data.front();
        }
    }
    //队头元素如果刚刚好是val，那么删掉它！
    void popIsVal(int val);
    {
        if( ( !data.empty() && val==data.front() )
        {
            data.pop_front();
        }
        
        return ;
    }
    
private:
    deque<int> data;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39