# 数学模板
# 目录
[TOC]
# 1.素数筛法
- 素数暴力到欧拉筛法
本文讲解了素数 的定义 并且从素数的暴力算法一路优化到了欧拉筛法
# 1.1.素数的定义
维基百科定义:
质数(Prime number),又称素数
指在大于1的自然数中,除了1和该数自身外,无法被其他自然数整除的数(也可定义为只有1与该数本身两个正因数的数)。大于1的自然数若不是素数,则称之为合数(也称为合成数)。
Tips:
1.有的教材上:(指在大于1的自然数中)这一点没有强调,导致容易误解!!!
也是经常弄晕一些人对素数的理解的原因。
2.所以:1既不是素数也不是合数!!!
# ✅素数相关算法
# 判别素数的朴素法(暴力法)
# 1)算法原理:
不管三七二十一 根据素数定义就是一顿暴力。
# 2)实现(轻微优化)
# 代码段:
int isPrime(int n)
{
//0表示不是素数,1表示是素数
if(n<=1)
return 0;
//表示根号n向下取整
int sqrt_num=(int)sqrt(1.0*n);
for(int i=2;i<=sqrt_num;i++)
{
if(n%i==0)
{
return 0;
}
}
return 1;//是素数
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 埃塞托尼亚筛
# 1)算法原理:
1>假设从2-N全是素数
2>从2开始枚举,对于每个素数,我们筛去它的所有倍数,最后我们剩下来的就都是素数
关键点:
从2开始枚举到某个数字A,如果a没有被前面步骤的数筛去,那么a一定是素数。
原因:
如果A(A>2)是合数,则A=素数×另一个数
PS:这个素数必定小于A,所以会被我们前面筛出来的素数筛掉
# 2)实现
用一个标记数组实现 枚举的过程中,筛的过程就是依次改变这个标记数组的过程
# 实现1:按照思路直接筛,筛的过程如下图红色箭头所示
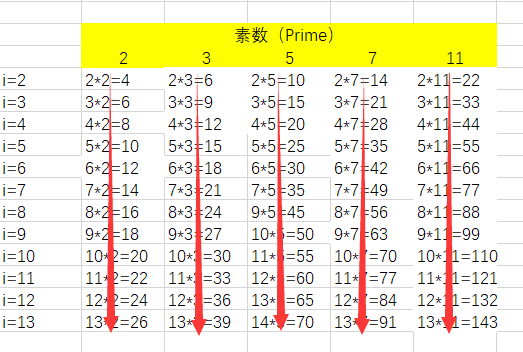
# 代码段:
//Eratosthenes_one.cpp
#include<cstdio>
const int maxn=100000+5;
//除了0,1之外(因为0和1既不是合数,也不是素数)
//TagArray数组中,0表示i是素数,1表示是合数
int TagArray[maxn]={0};
//Prime数组中存放素数(从0号位开始放)
//Num表示Prime数组中素数的个数
int Prime[10000+5]={0};
int Num=0;
void FindPrime()
{
for(int i=2;i<maxn;i++)
{
if(TagArray[i]==0)//如果标记数组说i这个数是素数
{
Prime[Num++]=i;//存素数i,并且Num+1
//注意这种写法,本来应该用i*j<=(maxn-1)判断就好了
//但是要避免i*j的结果溢出int,所以改为j<=((maxn-1)/i)
//maxn-1是因为标记数组范围本来就只有0-100004
for(int j=2; j<=((maxn-1)/i); ++j)
{
TagArray[j*i]=1;//筛去素数i的倍数
}
}
}
}
int main()
{
//求1-100000+4中哪些是素数
FindPrime();
printf("正整数100004内素数的个数:%d\n",Num);
for(int i=0;i<Num;i++)
{
printf("%d\n",Prime[i]);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# 实现2:
在实现1的基础上,我们发现,如图中蓝色部分的,被重复筛了。我们容易观察出,如果要减少筛的次数,我们可以从质数的平方往后筛(优化)
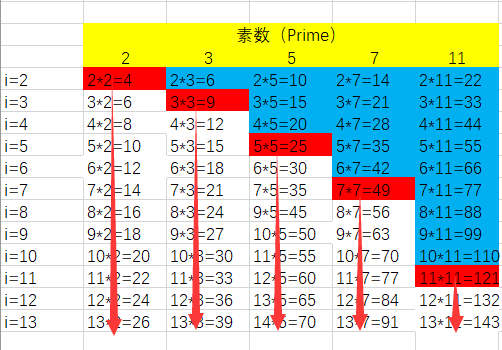
# 代码段:
//Eratosthenes_two.cpp
#include<cstdio>
const int maxn=100000+5;
//除了0,1之外(因为0和1既不是合数,也不是素数)
//TagArray数组中,0表示i是素数,1表示是合数
int TagArray[maxn]={0};
//Prime数组中存放素数(从0号位开始放)
//Num表示Prime数组中素数的个数
int Prime[10000+5]={0};
int Num=0;
void FindPrime()
{
for(int i=2;i<maxn;i++)
{
if(TagArray[i]==0)//如果标记数组说i这个数是素数
{
Prime[Num++]=i;//存素数i,并且Num+1
//注意这种写法,本来应该用i*j<=(maxn-1)判断就好了
//但是要避免i*j的结果溢出int,所以改为j<=((maxn-1)/i)
//maxn-1是因为标记数组范围本来就只有0-100004
//(修改处)将j=2改为了j=i,这样就能少筛掉表格中那些蓝色部分了
for(int j=i; j<=((maxn-1)/i); ++j)
{
TagArray[j*i]=1;//筛去素数i的倍数
}
}
}
}
int main()
{
//求1-100000+4中哪些是素数
FindPrime();
printf("正整数100004内素数的个数:%d\n",Num);
for(int i=0;i<Num;i++)
{
printf("%d\n",Prime[i]);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# 欧拉筛
由来: 由于埃塞托尼亚筛筛的时候重复筛(比如下面的)了,使得算法效率还不够好,所以,我们改进一下,我们继续观察先前的图,发现埃塞托尼亚筛是竖着筛,我们似乎也难以优化这种筛法了,我们转换一下思路——横着筛
# 1)算法原理:
思路:在埃氏筛的一种优化
任何合数都能写成一个素数乘一个数(显然这个素数不一定是唯一的)
//举个例子:12=26=34(2和3都是素数)
所以,任何合数都有一个最小的质因数
| 用这个"最小质因数"来判断什么时候不用继续筛下去 |
那么如何实现呢?
欧拉研究发现,我要是横着筛就会比前面那种只优化掉蓝色部分的埃氏筛还快
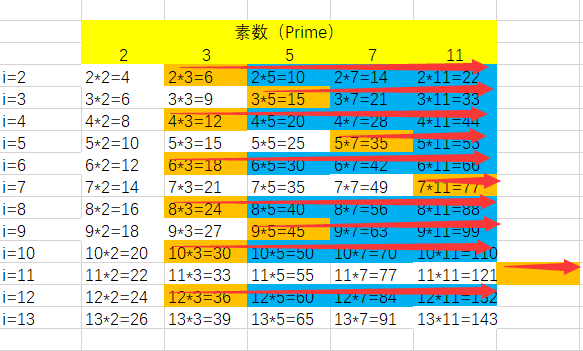
注意:这里是横着筛,此外图中箭头从橙色出发(包括该点)往右的所有我都不筛
具体实现方法是用的一个break实现的。
# 2)实现
# 代码段:
//Euler.cpp
#include<cstdio>
const int maxn=100000+5;
//除了0,1之外(因为0和1既不是合数,也不是素数)
//TagArray数组中,0表示i是素数,1表示是合数
int TagArray[maxn]={0};
//Prime数组中存放素数(从0号位开始放)
//Num表示Prime数组中素数的个数
int Prime[10000+5]={0};
int Num=0;
void FindPrime()
{
for(int i=2;i<maxn;i++)
{
if(TagArray[i]==0)//如果标记数组说i这个数是素数
{
Prime[Num++]=i;//存素数,并且Num+1
}
for(int j=0;(j<Num)&&(i<=((maxn-1)/Prime[j]));++j)
{
//一进来,不管三七二十一,先筛掉一个先
TagArray[i*Prime[j]]=1;
if(i%Prime[j]==0)
{
//判别i是Prime数组中某个的倍数,则跳出,
//这行后面的也不用筛
break;
}
}
}
}
int main()
{
//求1-100000+5-1中哪些是素数
FindPrime();
printf("正整数100004内素数的个数:%d\n",Num);
for(int i=0;i<Num;i++)
{
printf("%d\n",Prime[i]);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# 2.快速幂
- 求ab%m
- 下面的式子还使用了『同余定理』
long long LLow(long long a, long long b, long long m)
{
long long ans=1;
while( b>0 )
{
//如果b是偶数
if( b&1 )
{
ans=ans*a%m;
}
a=a*a%m;
b>>=1;
}
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 3.斯特林数(Stirling)
# 1.题目:
Number lengths
Time Limit: 1000ms, Special Time Limit:2500ms, Memory Limit:32768KB
Total submit users: 1411, Accepted users: 1317
Problem 10146 : No special judgement
Problem description
N! (N factorial) can be quite irritating and difficult to compute for large values of N. So instead of calculating N!, I want to know how many digits are in it. (Remember that N! = N * (N - 1) * (N - 2) * ... * 2 * 1)
Input
Each line of the input will have a single integer N on it 0 < N < 1000000 (1 million). Input is terminated by end of file.
Output
For each value of N, print out how many digits are in N!.
Sample Input
1
3
32000
1000000
Sample Output
1
1
130271
5565709
Problem Source
UD Contest
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# AC代码1
//考点:数学
//打表技巧
//注意点,关于如何弄出精度,
//原先想到的是斯特林公式,但是后面发现,都不需要这个
#include<cstdio>
#include<cmath>
const int maxn=1000000+5;
double a[maxn];
void init()
{
a[1]=1;
for(int i=2;i<maxn;++i)
{
//主要的保证精度的地方
a[i]=a[i-1]+log10(1.0*i);
}
}
int main()
{
init();
int n;
while(~scanf("%d",&n))
{
printf("%d\n",(int)a[n]);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
总结: 刚开始以为可以递归找规律,结果半点也没找出来0.0
- 注意:log10(x)就是求x的十进制位数,log(x)就是求x的二进制位数
其他人的想法:
- 刚刚听大神说这题维护前11位也可以过,可是我比赛时想的只是维护首位,然后发现到十几的时候就错了,所以就放弃了
# AC代码2
给出一个数N,求出N!的位数。 暴力法肯定是不行的,阶乘是个增长速度 很快的函数,10!已经有7位了。
更直接的方法是log10(N!) --以10为底N!的对数。 因为求位数就是要每次除以10 的,取对数的意义就是10的几次方才能到N!,也就是求了N!有几位。
那么问题就转化成求log10(N!)了
一种方法是换底公式然后求和log10(N!) = log2(1*2*3*..*N)/log2(10)分子拆开求和
2
# 精度问题
#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
int main()
{
int n,m;
scanf("%d",&n);
while(n--)//数据组数
{
scanf("%d",&m);
int ans = 0;
double a=0,b;
for(int i = 1;i<=m;i++)
a+= log(i);
a/= log(10);
ans = (int)a;
printf("%d\n",ans+1);//实践证明不+1总是少一位,大概是double舍入的问题?
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
此外,还有斯特林公式,也可以用来估计一些数字,OJ崩了,待补。
# 2.斯特林公式
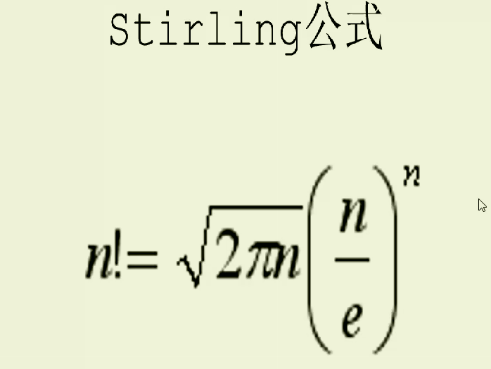
# OJ数学题
Reduced ID Numbers
Time Limit: 2000ms, Special Time Limit:2500ms, Memory Limit:32768KB
Total submit users: 624, Accepted users: 574
Problem 10275 : No special judgement
Problem description
T. Chur teaches various groups of students at university U. Every U-student has a unique Student Identification Number (SIN). A SIN s is an integer in the range 0 ≤ s ≤ MaxSIN with MaxSIN = 106-1. T. Chur finds this range of SINs too large for identification within her groups. For each group, she wants to find the smallest positive integer m, such that within the group all SINs reduced modulo m are unique.
Input
On the first line of the input is a single positive integer N, telling the number of test cases (groups) to follow. Each case starts with one line containing the integer G (1 ≤ G ≤ 300): the number of students in the group. The following G lines each contain one SIN. The SINs within a group are distinct, though not necessarily sorted.
Output
For each test case, output one line containing the smallest modulus m, such that all SINs reduced modulo m are distinct.
Sample Input
2
1
124866
3
124866
111111
987651
Sample Output
1
8
Problem Source
NWERC 2005
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 考点:同余定理
这道题是对同余定理的考查,思路很简单,暴力地枚举j,直到j满足集合中任意两个数对j取余都不相等,此时停止循环;
对于代码中的memset,比用for循环初始化为0快,只是在数组大的时候。在数组大小比较小时则for初始化比较省时(我在这超时了4、5次了)
一共是n个学生,所以去完模之后至少要有n个不同的值,所有程序里面的j要从n开始的。当然从1开始也不会错,只是一个小小的优化吧。
代码如下:
#include <stdio.h>
#include <string.h>
#include <math.h>
int a[10000001];
int main()
{
int i,j,n;
int cas,ans,t;
int s[303];
int f;
scanf("%d",&cas);
while(cas--)
{
scanf("%d",&n);
for(i=0;i<n;i++)
scanf("%d",&s[i]);
for(j=n;j<1000000;j++)
{
f=0;
for(i=0;i<=j;i++) //这里用memset的话会超时的!
a[i]=0;
for(i=0;i<n;i++)
{
if(a[s[i]%j])
{
f=1;
break;
}
a[s[i]%j]=1;
}
if(!f)
break;
}
printf("%d\n",j);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
- 湖大OJ上还能用gets『2020年记载的』
# 3.马拉车算法『模板』
- Manacher『马拉车算法』
- 2020-07-16
- 一种求最长回文串的线性算法
# 3.1.马拉车算法杂谈
1)利用对称性来降低时间复杂度 2)可以看做是中心拓展法的一种优秀的剪枝 3)马拉车算法可以在线性时间内找出以任何位置为中心的最大回文串
# 3.2.代码实现

参考链接:电子科技大学38min左右 (opens new window)
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN=110010;
char Ma[MAXN*2];//预处理后的字符串
int Radius[MAXN*2];//以其为中心的回文的半径Radius
void Manacher(char s[],int len)
{
int l=0;
Ma[l++]='$';
Ma[l++]='#';
for(int i=0;i<len;++i)
{
Ma[l++]=s[i];
Ma[l++]='#';
}
Ma[l]=0;//其实是对字符数组的收尾,'\0'
//______________________________核心代码begin
//center表示回文串的中心点
int right=0,center=0;
for(int i=0;i<l;++i)
{
//利用对称性,进行剪枝
Radius[i]=right>i?min(Radius[2*center-i],right-i):1;
//从中心往两边扩展
while(Ma[i+Radius[i]]==Ma[i-Radius[i]])
{
Radius[i]++;
}
//获取当前最长回文串的中心center和右侧最右边right
if(i+Radius[i]>right)
{
right=i+Radius[i];
center=i;
}
}
//______________________________核心代码end
}
char str[MAXN];
int main()
{
while(scanf("%s",str)==1)
{
int len=strlen(str);
Manacher(str,len);
int ans=0;
for(int i=0;i<2*len+2;++i)
{
ans=max(ans,Radius[i]-1);//回文长度和Radius[]的关系正好为-1(可以证明)
}
printf("%d\n",ans);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
另外的
#include <vector>
#include <iostream>
#include <string>
using namespace std;
string Mannacher(string s)
{
//插入"#"
string t="$#";
for(int i=0;i<s.size();++i)
{
t+=s[i];
t+="#";
}
vector<int> p(t.size(),0);
//mx表示某个回文串延伸在最右端半径的下标,id表示这个回文子串最中间位置下标
//resLen表示对应在s中的最大子回文串的半径,resCenter表示最大子回文串的中间位置
int mx=0,id=0,resLen=0,resCenter=0;
//建立p数组
for(int i=1;i<t.size();++i)
{
p[i]=mx>i?min(p[2*id-i],mx-i):1;
//遇到三种特殊的情况,需要利用中心扩展法
while(t[i+p[i]]==t[i-p[i]])++p[i];
//半径下标i+p[i]超过边界mx,需要更新
if(mx<i+p[i]){
mx=i+p[i];
id=i;
}
//更新最大回文子串的信息,半径及中间位置
if(resLen<p[i]){
resLen=p[i];
resCenter=i;
}
}
//最长回文子串长度为半径-1,起始位置为中间位置减去半径再除以2
return s.substr((resCenter-resLen)/2,resLen-1);
}
int main()
{
cout<<Mannacher("12212")<<endl;
cout<<Mannacher("122122")<<endl;
cout<<Mannacher("noon")<<endl;
system("pause");
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# 4.求众数『模板』
- 易错:摩尔投票法『仅能』解决非数学上的众数!
# 4.1.『众数的广泛例子』
比如,1,1,1,2,2,3,3,应该返回1而不是3『如果是摩尔投票法,会返回3』
『注意:摩尔投票法无法解决“数学上”的众数!!!!』
- 解法:哈希+遍历。。。
# 4.2.面试题 17.10. 主要元素 (opens new window)『众数的特例』
注意:使用摩尔投票法
相同意思的题目:169. 多数元素 (opens new window)
pairing阶段必然返回数组中的一个众数,但是由于众数不止一个,所以还需要经过counting阶段确认是否存在主要元素。
数组中占比『『超过一半』』的元素称之为主要元素。给定一个整数数组,找到它的主要元素。若没有,返回-1。
- 注意:这个是特例:因为1,1,1,2,2,3,3,3就只能返回-1了『和数学中的概念不一样』
- 此外,由于1/2,显然,我们排序后获取中间的数字也是OK的。。
# 摩尔投票法讲解:
- 核心:一组是众数!一组是奇奇怪怪的各大阵营的敌军!
class Solution {
public:
int majorityElement(vector<int>& nums) {
int CurNumMode=0x3f3f3f;
int count=0;//表示我方已经开始『领旗』,但是根基不稳
for( auto n : nums )
{
if( CurNumMode==n )
{
++count;
}
else
{
//根基不稳的可以被取代
if( 0==count )
{
CurNumMode=n;
//下面的代码『故意写,用来强化意思』
count=0;//表示我方已经开始『领旗』,但是根基不稳
}
else
{
--count;
}
}
}
int Len=nums.size();
int sum=0;
for( auto n : nums )
{
if( CurNumMode==n )
{
++sum;
}
}
if( sum>(Len/2) )
{
return CurNumMode;
}
else
{
return -1;
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 4.3.『众数的特例+特例』229. 求众数 II (opens new window)
- 给定一个大小为 n 的整数数组,找出其中所有出现超过
⌊ n/3 ⌋次的元素。
『可以对』摩尔投票算法进行改进: