3种线性排序

目录

• 目录
  • ✅前述
  • ✅计数排序（counting sort）读音是第4声
  • 1.假设和操作
  • 2.算法分析
  • 3.局限性
  • ✅基数排序（Radix sort）读音是第1声
  • 1.操作
  • 2.疑问
  • 3.算法分析
  • ✅桶排序（bucket sort）
  • 1.假设和操作：
  • 2.算法分析
  • ✅联系和总结

[TOC]

✅前述

《算法导论》中提到有定理表明：

• 任何比较排序在最坏的情况下都要经过O(nlogn)次比较

下面讨论三种线性时间复杂度的排序算法。

• 原因：这三种算法是用运算而不是比较来确定排序顺序的，所以能够突破这个定理的桎梏

排序算法4问：

• 1)时间复杂度

• 2)空间复杂度

• 3)排序是否原地

  • 原地排序：指不需要开辟额外空间

• 4)稳定性

  • 稳定的排序：具有相同值的元素在输出数组中的相对次序与他们在输入数组中的相对次序相同
  • 意义：只有当进行排序的数据还附带"卫星数据"时才比较重要。 eg.我们排序的是结构体的整数值，而整数值相同的，可能他的字符串不同。

✅计数排序（counting sort）读音是第4声

1.假设和操作

『输入数据假设』

假设n个输入元素中的每个元素都是在[min,max]区间的一个整数。 排序快的原因：

• 进行了上面的假设

• 用空间换时间

『操作』

• 1·建立一个长度为max-min+1的统计数组，元素初始化为0
• 2·每次扫描进数据，那么对应的统计数组的值+1（数组每一个下标位置的值，代表了数列中对应整数出现的次数）（计数一词的来源）
• 3·遍历统计数组，输出数组元素的下标值，元素的值是几，就输出几次
• 4·如果排序的带有"卫星数据",则需要进行第4步————此举，保证了计数排序的稳定性

• 对已经填充完的统计数组，做一下变形——具体的请见下面场景
• 根据情况，选择正向或者反向遍历统计数组

Tips：计数排序的稳定性很重要的另一个原因是：计数排序经常会被用作基数排序算法的一个子过程，为了使基数排序正确执行，计数排序必须是稳定的。

创造场景如下：

• 假设有一个企业的招聘系统规则如下

• 申请者需要投递简历，写好姓名，将得到一个原始的排名Ranking
• 为了激励大家投递简历，发布了一条通知,我们的排名（Ranking）依据两个维度来给申请者面试名额

• 1.笔试成绩高者，排名（Ranking）高
• 2.笔试成绩相同者，公司会给先投递简历的人高的排名（Ranking）
  此处体现了，排序的稳定性需求
• 我们最后会将排名（Ranking）前4的申请者的名字（name）打印出来
  名字是我们要排序的成绩（grade）的卫星数据

申请者的结构体设计如下

struct Apply
{
	char name[20];
	int grade;
}Ranking[1000];

显然，我们的计数排序是根据结构体的元素，grade来排名。 此外，为了容易说明计数排序，我们假设，笔试成绩范围是0-10分 投递简历如下图：

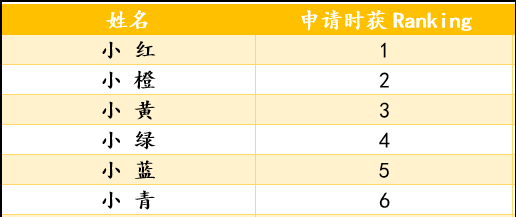
• 笔试完了，成绩如下图：

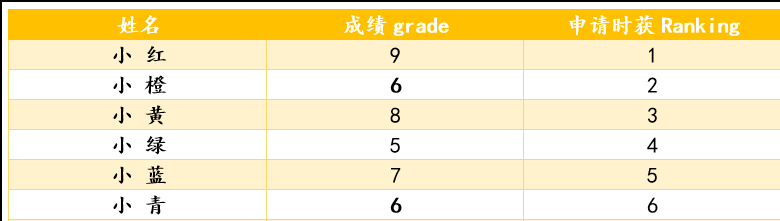
请按照规则给上面排序，注意：小橙和小青的成绩都是6 操作： 1·建立一个长度为11的统计数组，元素初始化为0，表示我们的成绩为0-10 2·每次扫描进数据，那么对应的统计数组的值+1 显然获得统计数组如下图：

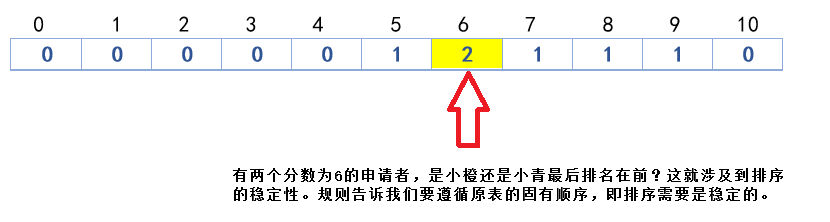
3.暂时，不需要输出 4.对统计数组进行变形： 方法，从倒数第2位开始，反向遍历统计数组，a[i]=a[i+1]+a[i]; 相加的目的,是为了让统计数组存储的元素值,等于相应grade的排名的最终排序位置。

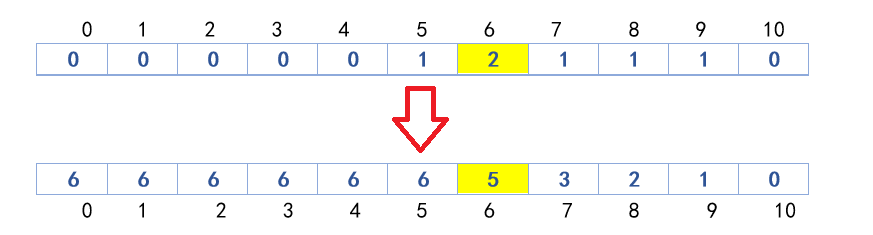
5.接下来,我们创建输出数组,长度和输入数组一致。 然后

注意1）从后往前遍历

原先的输入数组 小青，成绩6，查统计数组,值为2（有2个同成绩的），查变形后数组，放输出数组第5位 Tips：查到统计数组值为2，我们在放完小青到输出数组之后，需将变形后的数组的值减1，变成了4

注意2）从5变成4,代表着下次再遇到6分的成绩时,最终排名是第4。（这就保证了计数排序的稳定性!）

小蓝，成绩7,查统计数组,值为1（唯一），查变形后的数组，放输出数组的第3位 小绿，成绩5,查统计数组,值为1（唯一），查变形后的数组，放输出数组的第6位 小黄，成绩8,查统计数组,值为1（唯一），查变形后的数组，放输出数组的第2位

小橙，成绩6,查统计数组,值为2（有2个同成绩的），查变形后数组，知放输出数组第4位 我们在放完小橙到输出数组之后，需将变形后的数组的值，减1，变成了3

小红,成绩9,查统计数组,值为1（唯一），查变形后的数组，知放输出数组的第1位

排序后结果（如图，保证了卫星数据的稳定性）：

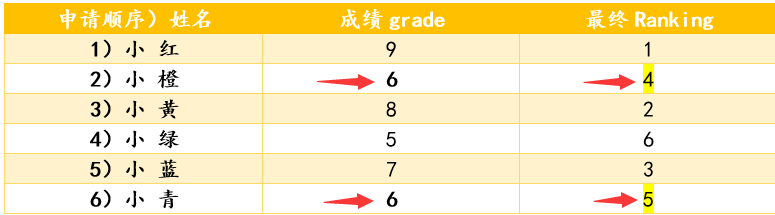
2.算法分析

• 时间复杂度：O(n+m)其中m是原始数组的整数范围

• 空间复杂度：O(n+m)

• 是否原地排序：否

• 稳定性：稳定

• 数据结构：数组，hash

Tips：有人也把统计数组的每个位置，叫做一个个桶，但我们暂时不这么叫，免得大家将桶排序和计数排序弄混了

3.局限性

• 1.当输入数组元素最大最小值差距过大时 比如给定20个随机整数,范围在0到1亿之间,这时若使用计数排序,需创建长度为1亿的数组。严重浪费空间,且时间复杂度也随之升高。 解决方案：见桶排序
• 2.当输入数组元索不是整数，如字符，浮点数

• 如果数列中的元素都是小数,比如25.23 ,或是0.01这样子,无法创建对应的统计数组。 解决方案1：假如是0.3,0.13,0.001,0.22 我们可以将他们全乘1000，然后就转换为计数排序，输出的时候，记得除回来 解决方案2：见桶排序
• 如果数列中的元素都是字符或字符串,比如abc,b,c 解决方案1：借助字符的ASCII码，按位赋权，转换hash为数字，再排序 解决方案2：见基数排序，借助字符的ASCII码。

• 4.如果，输入的元素是大整数，比如15位长的号码1234567894554541,可是,15位长的号码有多少种组合?这要建立一个大得不可想象的数组,才能装下所有可能出现的15位长的号码，很不划算! 解决方案：见基数排序（思想：减而治之）
• 5.其他————碰到了再补充，总之，要灵活运用，而不是将某种算法运用场景当做教条，场景只是帮助更好的理解算法的一种方式。

✅基数排序（Radix sort）读音是第1声

1.操作

需求：为如下一组英文单词排序

操作：我们把排序工作拆分成多个阶段,每一个阶段只根据一个字符(基数排序，基字的由来)进行计数排序, 一共排序k轮, k是元素长度。 如何将这些字符串按照字母顺序排序呢? 具体的 由于每个字符串的长度是3个字符,我们可以把排序工作拆分成3轮

• 第一轮:按照最低位字符排序。排序过程使用计数排序,把字母的ascii码对应到数组下标，第1轮排序结果如下:

• 第二轮:在第一轮排序结果的基础上,按照第二位字符排序，第2轮排序结果如下:

• 注意：这里使用的计数排序必须是稳定排序,这样才能保证第1轮排出的先后顺序在第2轮还能继续保持！
• 比如，在第1轮排序后,元素uue在元素yui之前。那么第二轮排序时,两者的第二位字符虽然同样是u,但先后顺序一定不能变,否则第1轮排序就白做了。

• 第三轮：同理，略。

  • 基数排序(Radix Sort)：形如这样把字符串元素按位拆分,每一个基位进行一次稳定性的排序的算法,就是基数排序
  • 基数排序既可以从高位优先进行排序（Most Significant Digit first ,简称MSD ）
  • 也可以从低位优先进行排序（Least Significant Digit first ,简称LSD）
  • 刚才我们所举的例子,就是典型的LSD方式的基数排序。

2.疑问

问：如果排序的字符串长度不规则呢? 比如有的字符串是5位，有的是3位

banana
apple
orange
ape
he

毛主席说过，没有条件，我们就创造条件 创造条件： 我们以最长的字符串为准，其他长度不足的字符串，在末尾补0即可

banana
apple0
orange
ape000
he0000

在排序时,我们把字符0当做是比a更小的字符,排序结果如下:

ape000
apple0
banana
he0000
orange

3.算法分析

• 时间复杂度：O(k(n+m)) 其中m是原始数组的整数范围 由于字符串元素的长度k是一个固定常量，所以我们认为这个是一个线性的排序算法。
• 空间复杂度：O(n+m) 至于空间复杂度，由于基数排序的辅助数组是反复重用的，所以基数排序的空间复杂度和计算排序一样。
• 是否原地排序：否
• 稳定性：稳定
• 数据结构：数组，hash

注意点：

• 1.上面的算法时间复杂度分析是不够完善的，其实上面的是以计数排序这种稳定排序作为基数排序的子过程的复杂度分析。基数排序，其实主要是强调，我们对待一些排序，可以按位（比如，我们二进制中，按照以2为基的任何位），来分别排序。
• 2.推而广之：基数排序的子过程，可以是任何具有稳定性的排序算法（注意点）
  • eg.插入排序，折半插入排序，冒泡排序
  • Tips:其实，基数排序的算法的时间复杂度分析依赖于我们所使用的稳定的排序算法！！！

✅桶排序（bucket sort）

1.假设和操作：

• 碎碎念：桶排序同样是一种线性时间的排序算法。类似于计数排序所创建的统计数组，桶排序需要创建若干个桶来协助排序。这也大概是为什么有的人，将计数排序中的统计数组的叫做一个个桶的原因吧，然后推而广之，也在基数排序中叫桶
  • 殊不知：有时就是这样的叫法把初学者弄混了，不知道，是不是有桶的都叫桶排序？
  • 其实，《算法导论》一书中，并没有把计数排序和基数排序中的统计数组叫桶...

但是，其实桶排序体现的是一种思想，我们不用纠结的是"桶"到底是什么，我们需要的是根据实际情况去选择合适的数据结构去存储，实现这个抽象的"桶"，所以，我们也将计数和基数排序中的统计数组算做是"桶"点一种实现方式吧。

与计数排序相似，因为对输入数据进行了某种假设，桶排序的速度也很快。 假设：输入数据服从均匀分布

那么,桶排序当中所谓的"桶”，又是什么概念呢? 每一个桶(bucket)代表一个区间范围,里面可以承载一个或多个元素。

• 操作：
  • 第一步，就是创建这些桶,确定每一个桶的区间范围
  • 第二步，将创建这些桶,分别都进行排序处理（由于，数据满足均匀分布，所以，我们的每个桶放的元素应该都差不多一样多，也就是均匀）
  • 第三步，合并桶，进行输出

2.算法分析

假设原始数列有n个元素,分成m个桶, 平均每个桶的元素个数为n/m。 下面我们来逐步分析算法复杂度:

• 第一步，求数列最大最小值,运算量为n。
• 第二步，创建空桶,运算量为m。
• 第三步，遍历原始数列,运算量为n。
• 第四步，在每个桶内部做排序,若是使用了$0(nlogn)$的排序算法,所以运算量为 $n/m * log(n/m)* m$
• 第五步,输出排序数列,运算量为n。 加起来,总的运算为$3n+m+ n/m * log(n/m)* m = 3n+m+ n(logn-logm)$ 去掉系数,时间复杂度为: O(n+m+n(logn-logm) )

空间复杂度: 空桶占用的空间+数列在桶中占用的空间=O(n+m)

• 时间复杂度：O(n+m+n(logn-logm))
• 空间复杂度：O(n+m)
• 是否原地排序：否
• 稳定性：若是桶内使用不稳定的排序，则不稳定，但是桶与桶之间是稳定的
• 数据结构：数组，链表，堆...看场景

Tips：分析

• 时间复杂度：

  • 最坏n方（一个桶)）
  • 最好为n（n个桶而且值排列均匀）

• 空间复杂度：

  • 其实，要是想要空间复杂度最好，得用链表，但是那样时间复杂度就做不到最好

✅联系和总结

总的来说，计数排序，基数排序，桶排序都是用的空间换取时间的思想。 另外，我们的计数排序和基数排序都可以看做是桶排序，"桶思想"的一种特例。

• 由于，桶排序的复杂度分析很依赖于具体的数据，我们常用的反而是计数排序和基数排序。

• 从桶排序的算法分析中，我们需要知道的是，没有绝对高效的算法，只有合适的算法应用场景！

• 总的说来，算法的设计，一般体现的是用时间换空间，或者空间换时间。