# DP动态规划
<font style="background:yellow">
- 1.DP和数学找规律题的区别
- 2.dp的递归写法、迭代写法
- 3.背包九讲阅读
参考OI进行分类
1)记忆化搜索
2)背包 DP
3)区间 DP
4)树形 DP
5)DAG 上的 DP
6)状压 DP
7)数位 DP
8)插头 DP
9)计数 DP
10)动态 DP
11)DP 优化
2
3
4
5
6
7
8
9
10
11
12
# 📑 目录
[TOC]
# ✅动态规划思考模板
- 1、确定『状态』和『选择』:容易
- 状态:如何才能描述一个问题的局面?也就是会发生变化的『变量』
- 选择:每一步要做的决定
- 2、确定dp【状态1】【状态2】【状态3】。。。数组的意义
- 3、根据“选择”,思考状态转移的逻辑
- 确定Base问题,如何初始化
- 4、『自己决定要不要优化』
# 1.dp前置知识『找规律技巧』
# 1.1借助OJ设计原理技巧,输出编号
- Tips:
in.txt和out.txt都和你运行的程序在同一当前目录 - 首先,我创建in.txt作为,我存入输入数据
- 其次,我可以建立out.txt,也可不建立
# 1.1.1.模板如下
#include<stdio.h>
int main()
{
FILE * fp_in;
FILE * fp_out;
//输入文件,"r+"用读/写方式,打开一个(已存在)的文件
fp_in=fopen("in.txt","r+");
//输出文件,"w+"表示,用读/写方式,(建立)一个新的文本文件
//PS:其实,要是我原先建好了out.txt也行。
fp_out=fopen("out.txt","w+");
if(NULL==fp_in)
{
printf("NO");
}
else
{
int a,b,c;
int i=1;//用于编号
//这是对文件中的字符,用格式"%d%d%d"扫描进来。
while(~fscanf(fp_in,"%d%d%d",&a,&b,&c))
{
printf("%d %d %d\n",a,b,c);
printf("n=%d sum=%d\n",i,a+b+c);//编号
fprintf(fp_out,"n=%d sum=%d\n",i++,a+b+c);
}
}
fclose(fp_in);//关闭输入文件
fclose(fp_out);//关闭输出文件
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
Tips:测试样例
- 1.1.2.第一种输入,in.txt(我习惯用这样的)
1 3 5
2 6 10
4 12 20
//in.txt
2
3
4
5
- 1.1.3.第二种输入
in.txt(这样也行)
1 3 5 2 6 10
4 12 20
//in.txt
2
3
4
- 1.1.4.输出的
out.txt
n=1 sum=9
n=2 sum=18
n=3 sum=36
//out.txt
2
3
4
5
# 1.2.技巧的使用案例
# 1.2.1.例1:XOR sum
(不是动态规划)
考察知识点:
前缀和,位运算湖南大学程序设计竞赛新生赛
M题XOR sum (opens new window)小范围暴力找规律,规律当结论记住`
题目描述
You are given two positive integers l and r,you shoud answer l⊕(l+1)⊕...⊕r,where ⊕ denotes the bitwise XOR operation. In XOR operation we perform the comparison of two bits, being 1 if the two bits are different, and 0 if they are the same.
For example:
输入描述:
The input contain two integers l ,r (1 ≤ l ≤ r ≤1018)
输出描述:
The only output line should contain a single integer
示例1
输入
1 2
输出
3
说明
1⊕2=3
示例2
输入
3 6
输出
4
说明
3⊕4⊕5⊕6=4
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- 『1。。思路:』
1)想法1:首先看到能够很明显模拟的,那么首先就会想到暴力,但是会发现TLE
2)想法2:这样,很有规律但是超时的,那么可能是**规律题,或者可能是动态规划,
那么问题转换为如何找规律,或者如何找状态转移方程**
- 『2。。做法』
1)首先创建测试数据,为了避免手工输入测试数据太慢,也避免测试数据太少,无法找出规律,所以,我写了代码生成in.txt
#include<cstdio>
int main()
{
FILE * fp_in;
fp_in=fopen("in.txt","w+");
for(int i=1;i<101;++i)
{
fprintf(fp_in,"1 %d\n",i);
}
fclose(fp_in);
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
- 生成的
in.txt中,有形如这样的
1 1
1 2
1 3
1 4
1 5
省略-——注意,这不是文件中的
1 100
2
3
4
5
6
7
2)准备数据进行小范围的OJ模拟
代码
#include<cstdio>
int main()
{
FILE * fp_in;
FILE * fp_out;
fp_in=fopen("in.txt","r+");
fp_out=fopen("out.txt","w+");
unsigned int a,b;
int n=1;
while(~fscanf(fp_in,"%u%u",&a,&b))
{
unsigned sum=a;
for(unsigned int i=(a+1);i<=b;++i)
{
sum^=i;
}
fprintf(fp_out,"%d-%d ==%d\n",a,b,sum);
}
fclose(fp_in);
fclose(fp_out);
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
模拟出out.txt
1-1 ==1
1-2 ==3
1-3 ==0
1-4 ==4
1-5 ==1
1-6 ==7
1-7 ==0
1-8 ==8
1-9 ==1
1-10 ==11
1-11 ==0
1-12 ==12
1-13 ==1
1-14 ==15
1-15 ==0
1-16 ==16
1-17 ==1
1-18 ==19
1-19 ==0
1-20 ==20
1-21 ==1
1-22 ==23
1-23 ==0
省略-——注意,这不是文件中的
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
显然,有比较明显的规律如下图
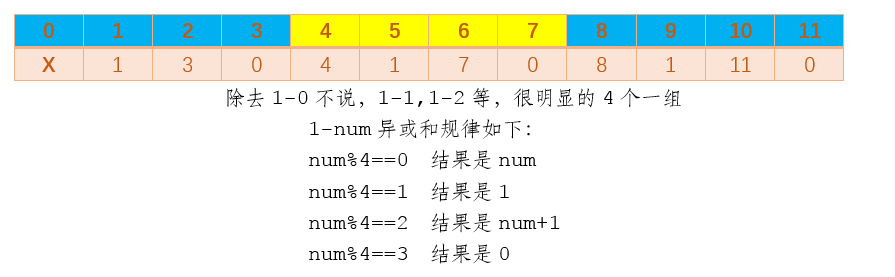
- 至此,我们发现了1-num的规律,由于规律太明显,不经让人大胆的猜测,其他形如2-num,3-num可能都只与
区间[left,right]的right有关,但是我们要严谨,毕竟,现在暴力模拟的只是
left=1的场景
# 3)《一》常规方式
(虽然技巧性没有那么强,但是比较通用)
我们可以有两种做法,但是其实都是殊途同归
1)直接用这个模拟,然后,我们手算测试2-num,3-num。差不多的话,那就比较肯定是这个规律
1)模拟2-num,模拟3-num等,综合几组找规律
但是,由示例2的3-6发现,也并不满足这个规律,第1种比较碰运气的不行。
但是由于有这么明显的规律,那么我们不妨用第2种做法,我们还是很相信,最后结果和left可能也有关。
再次暴力模拟
2-2 ==2
2-3 ==1
2-4 ==5
2-5 ==0
2-6 ==6
2-7 ==1
2-8 ==9
2-9 ==0
2-10 ==10
2-11 ==1
2-12 ==13
2-13 ==0
2-14 ==14
2-15 ==1
省略----
2
3
4
5
6
7
8
9
10
11
12
13
14
15
显然,又是4个一组
并且又是下面这样的规律,但是却和1-num的编号,对不上。
num
1
num+1
0
2
3
4
模拟3-num
3-3 ==3
3-4 ==7
3-5 ==2
3-6 ==4
3-7 ==3
3-8 ==11
3-9 ==2
3-10 ==8
3-11 ==3
3-12 ==15
3-13 ==2
3-14 ==12
3-15 ==3
3-16 ==19
3-17 ==2
3-18 ==16
3-19 ==3
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
继续模拟,省略。。。后续,我对照
尴尬的。。。我没有找出规律。所以,我后面用的下面技巧性的方法想出来的。
# 4)《二》技巧性的方法
至此,懒得再次模拟,可以借助我以前写代码,比如说前n项和等开放的思维。
我就想,如何将[left,right]和[1,right]联系起来?
后来,笔者观察到的是这样的规律:
我们假设,$f(n)$表示[1,right]的异或和
那么,我们观察到
$f(3)=1^2^3$
$f(5)=1^2^3^4^5$
要是,我们想要求[3,5]的异或和
也就是求$f=3^4^5$
我们的目标就转换为,如何由前面两个式子弄成现在这个式子的样子
我首先想到的是,可以类似除法的话
那么,我需要的式子应该是
$f(2)=1^2$
$f(5)=1^2^3^4^5$
但是,又不能直接和除法一样除,灵机一转,那我从异或的角度来思考
异或规则:
0^1=1
0^0=0
1^0=1
1^1=0
相同则为0,不同则为1
2
3
4
5
如何才能将前面的$1^2$去掉呢,并且还不能影响到后面的呢
由异或的规则前两行,我们发现,0和k=0,1或都等于k
其实是如何求
$f=3^4^5$就可以转换为$f=0^3^4^5$
但是,问题又来了,前面的0如何构造。
灵机一转,任何两个相同的数字,异或永远是0。
那么,求$f=3^4^5$就可以转换为$f(3-1)^f(5)$
# 5)最终代码
#include<cstdio>
unsigned long long solution(unsigned long long n)
{
if(n%4==0)
return n;
else if(n%4==1)
return 1;
else if(n%4==2)
return n+1;
else if(n%4==3)
return 0;
}
int main(void)
{
unsigned long long a,b;
//注意,是正整数,然后,我先前只考虑的unsigned int,只通过了0.8样例
//后来发现,,,对了,unsigned long long。我怎么先前就假设别人要的unsigned int 呢
while(~scanf("%lld%lld",&a,&b))
{
printf("%lld\n",solution(a-1)^solution(b));
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 1.2.2.例2:统计累加算式
- (可以说是规律题,也可以说是dp题)
- 来源:深信服校园招聘
c/c++软件开发D卷 统计累加算式 (opens new window) - 也有来源说是 整数分解为2的幂 清华复试
- 考察知识点:
分区(数论)
示例1
输入
7
输出
6
2
3
4
# 1)思路
1)首先,想到暴力进行模拟,利用数组,下表i表示2的i次方,用数组值模拟个数。但是这种的搜索空间太大了
比如,题干举例的7,在1+1+1+4和1+2+2+2,显然,我们直接从全1,慢慢合并到最终的1+2+4,其中我们还需要进行回溯。比较麻烦,也比较容易超时。
2)从以前阅读的《具体数学》书中启发的,我们对于这种很有可能有规律的,进行找规律
3)进一步的,其实,我们方法1)是从全1开始合并到最终,那么我们可以反过来思考。从那个数字本身对应的二进制位,每个权,一步步分解,直到全1,这个其实也要回溯,但是这样反着分解,似乎有些猫腻。(具体见下)
# 2)找规律
手工模拟,分解
1的分解方法 有1种
1=1
2的分解方法 有2种
2=1+1 2
3的分解方法 有2种
4的分解方法 有4种
5的分解方法 有4种
6的分解方法 有6种
7的分解方法 有6种
至此,我就已经发现比较显然的几种可能的规律: 1)很肯定的规律:$f(2m+1)=f(2m)$(m=1,2,3...n) 2)猜测1:$f(2m)=2m$(m=1,2,3...n) 3)猜测2:$f(2m)=f((2m)/2)+f(2m-1)=f(m)+f(2m-1)$(m=1,2,3...n)
为什么说,规律1)我很肯定呢,因为,我做出猜测之后,能够很容易的证明这个猜想是对的 Reason:我们知道奇数的二进制的最低位肯定是1,偶数则是0 由此,我们知道,比起偶数,比他大1的相邻的奇数,肯定最后那个1无法合并,一直放在各个分解的式子末尾,所以不影响分解方法数目。
验证,猜测1)
我们将8进行分解
1+1+1+1+1+1+1+1 1+1+1+1+1+1+2 1+1+1+1+2+2 1+1+2+2+2 2+2+2+2 2+2+4 4+4 8
此外,我们回溯,1+1+1+1+2+2h还有
1+1+1+1+4 1+1+2+4
有10种
猜测1错误
验证,猜测2) 从验证猜想1时求的8点分解数,我们发现,由再次符合了我们的想法。 在实际编码的时候,或许我们这样就会直接用这个猜想去搏一搏了。 但是,我现在是在写博客2333,还是老实证明一下吧
老实说,至此,我第一次想的时候没有想出如何证明:
后来想的证明,也比这篇博客写的复杂
参考博客:https://blog.csdn.net/zhang20072844/article/details/17033931
所以此处,我想引用这篇博客的证明:
证明:
证明的要点是考虑划分中是否有1。
记:
A(n) = n的所有划分组成的集合,
B(n) = n的所有含有1的划分组成的集合,
C(n) = n的所有不含1的划分组成的集合,
则有: A(n) = B(n)∪C(n)。
又记:
f(n) = A(n)中元素的个数,
g(n) = B(n)中元素的个数,
h(n) = C(n)中元素的个数,
易知: f(n) = g(n) + h(n)。
我们先来证明: f(2m + 1) = f(2m),
首先,2m + 1 的每个划分中至少有一个1,去掉这个1,就得到 2m 的一个划分,故 f(2m + 1)≤f(2m)。
其次,2m 的每个划分加上个1,就构成了 2m + 1 的一个划分,故 f(2m)≤f(2m + 1)。
综上,f(2m + 1) = f(2m)。
接着我们要证明: f(2m) = f(2m - 1) + f(m),
把 B(2m) 中的划分中的1去掉一个,就得到 A(2m - 1) 中的一个划分,故 g(2m)≤f(2m - 1)。
把 A(2m - 1) 中的划分加上一个1,就得到 B(2m) 中的一个划分,故 f(2m - 1)≤g(2m)。
综上,g(2m) = f(2m - 1)。
把 C(2m) 中的划分的元素都除以2,就得到 A(m) 中的一个划分,故 h(2m)≤f(m)。
把 A(m) 中的划分的元素都乘2,就得到 C(2m) 中的一个划分,故 f(m)≤h(2m)。
综上,h(2m) = f(m)。
所以: f(2m) = g(2m) + h(2m) = f(2m - 1) + f(m)。
这就证明了我们的递推公式。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Tips:个人的一些感受
1)从找规律这一方面,或许能够解释说明,为什么我上次进行企业笔试的时候,会有找规律的题目
那是为了练习我们对于数字的敏感程度,比如碰到这样的题目,我们可以猜想出猜想1)和2)这两种。
但是,一般的,要是不锻炼,或许,我们就只会做出猜想1)就以为只有这种规律了,但是其实,猜想2)页可以解释,而且才是最正确的。
2)此外,也解释了,为什么,我们在做笔试的题目发现有的题目可能有2种及以上的猜想都似乎可以
那样,只是说明,你的数字敏感度和思维广度很不同,但是,遗憾的,有时候碰到那样,没有后续数据给你验证,
你可能就陷入了2个选项啥的纠结,这种情况,我碰到了几次,,,(个人觉得,那是笔试这种题目的缺陷之处,或许改为,先选,然后把思路写下来,提交,按照思路进行判卷,比单纯的选择题更好)
2
3
4
5
6
# 3)代码
# 写法1——递归
优点:简洁 缺点:数据大的时候,会由于调用栈太深,有问题
#include<stdio.h>
int solution(int n)
{
if(1==n)
{
return 1;
}
else if(n&1)//奇数
{
return solution(n-1);
}
else
{
return solution(n-1)+solution(n/2);
}
}
int main()
{
int n;
while(~scanf("%d",&n))
{
printf("%d\n",solution(n));
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 写法2—打表技巧
#include<cstdio>
const int maxn=100000+5;
int solution[maxn]={0};
void init()
{
solution[1]=1;
solution[2]=2;
solution[3]=2;
for(int i=4;i<maxn;++i)
{
if(i&1)
{
solution[i]=solution[i-1];
}
else
{
solution[i]=solution[i/2]+solution[i-1];
}
}
}
int main()
{
init();//讲所有的弄出来
int n;
while(~scanf("%d",&n))
{
printf("%d\n",solution[n]);
}
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
最后:
- 还有一篇文章讲解了用DP和DFS剪枝来做这题,非常棒
- 链接:
https://www.jianshu.com/p/216b692d32ea - 还有,发现自己的不足,进行补充知识点——分区(数论)-维基百科
# 2.dp基础⭐️
# 2.1.适用情况
维基百科:
- 1)最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。最优子结构性质为动态规划算法解决问题提供了重要线索。
- 2)无后效性。即子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响。
- 3)子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率,降低了时间复杂度。
# 2.2.动态规划解题的『一般思路』
- 可以参考这篇知乎 (opens new window)
- 还可以参考北大郭炜的两种『递推』的写法:“人人为我”和“为为人人”
# 2.3.动态规划思考和答疑
(1)动态规划的实现方式
- Q:动态规划只能用『递推』写嘛?
- A:不是的,动态规划可以用『递归』和『递推』这2种都可以,动态规划只是一个思考方式
(2)动态规划的常见写法有
- Q:动态规划的常见写法?
- A:比如下面5种方式
- 递归
- 递归改为栈来模拟
- 递推
- 递推+数组来辅助加速『备忘录写法』
- 递推+更少的数组辅助『滚动数组”优化』
其实动态规划将大事化下,小事化了的想法和“分治法”很像。
# 2.3.1动态规划中的系列概念
深刻理解下面两句话: 动态规划是一种解决问题的方法:多阶段“决策”。 动态规划是一种思想:大问题转换为小问题。
1)“备忘录写法”——其实就是将已经计划出来的数据保留下来,避免重复计算,可以说就是“打表技巧” 2)“滚动数组”优化——这是,其实是将状态转移的时候,需要借助的数据尽可能的减少,因为一般转移的时候,只需要临近的几个数据,并不需要全部的,“滚动数组”是一种减少空间复杂度的手段。 3)阶段和状态 4)DAG(有向无环图) 5)线性规划是一次性就
# 2.3.2.两种动态规划的解题思路(极客时间)
它们分别是状态转移表法和状态转移方程法。
其中,状态转移表法解题思路大致可以概括为,回溯算法实现 - 定义状态 - 画递归树 - 找重复子问题 画状态转移表 - 根据递推关系填表 - 将填表过程翻译成代码。
状态转移方程法的大致思路可以概括为,找最优子结构 - 写状态转移方程 - 将状态转移方程翻译成代码
九章算法
- 什么情况下使用动态规划?
- 满足下面三个条件之一, 则极有可能是使用动态规划求解
- 求最大值最小值
- 判断是否可行
- 统计方案个数
- 满足下面三个条件之一, 则极有可能是使用动态规划求解
# 3.DP的启发性思维导图
- 1.BFS本身就是一种DP
- 2.DP的2种写法:递归和递推(又叫迭代)
# 🍁参考资料
- 背包九讲 (opens new window)-
Tianyi Cui - 算法笔记-胡凡
- 从运筹学的数学角度讲“动态规划” (opens new window)
- 极客时间-数据结构与算法之美-王争
- OI.wiki (opens new window)
- 九章算法 (opens new window),GitHub