3.必备-工程常用算法
2025/12/29大约 12 分钟
3.必备-工程常用算法
目录
1.并查集UnionSet『模板』
1.1.模板题
- 剑指 Offer II 116. 朋友圈『纯模板题』
- 547. 省份数量『纯模板题』
1.2.最终ADT模板设计✔️
- 设计思想阐述:
- 1.初始化,所有节点的父节点都是自己『表示,我是一座孤岛』
- 2.merge,孤岛之间开始连接
- 2.1.如果纯粹连接,发现会可能出现『闭环』
- 2.2.为了解决闭环『我们需要设计一个函数』用于获得我们这块岛屿的岛主leader
//抽象数据类型(Abstract Data Type,ADT),也就是我们设计的『并查集』
class UnionSet
{
//1、内置『封装』的数据结构
private:
int num;//不连通分量
vector<int> parent;
//2、算法
public:
bool connected(int a, int b); //判断是否连通
int count(); //『必要』返回几个集合、也就是:判断有多少个不连通图
void merge(int first, int second);//『必要』合并集合
int findFather(int x); //『必要、必要性证明见后边』查找x在哪个集合,找最终父亲结构
UnionSet(int n):num(n) //『必要』
{
parent.resize(n);
};
};1.3.findFather函数存在的必要性证明:
- 并查集设计的坑
- 自己设计的并查集,存在闭环问题
- 剑指 Offer II 116. 朋友圈『纯模板题』测试如下
class UnionSet
{
public:
UnionSet(int n)
{
father.resize(n);
for(int i=0; i<n; ++i)
{
father[i]=i;
}
}
//出错的地方,就在于,merge的策略太简单,所以是不OK的
/*
[[1,1,1],[1,1,1],[1,1,1]]
输出
0 『错位』
预期结果
1
*/
void merge(int first, int second)
{
if( first>second )
{
swap(first,second);
}
if( father[first]==second ||father[second]==first )
{
return ;
}
if( father[first]!=first )
{
father[second]=first;
return ;
}
else //if( father[second]!=second )
{
father[first]=second;
}
}
int ret()
{
int res=0;
for(int i=0; i<father.size(); ++i)
{
if( father[i]==i )
{
++res;
//cout<<"ok"<<i<<endl;
}
}
return res;
}
private:
vector<int> father;
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int Len=isConnected.size();
if( 0==Len )
{
return 0;
}
UnionSet solve( Len );
for(int i=0; i<Len; ++i)
{
for(int j=0; j<i; ++j)
{
if( 1==isConnected[i][j] && i!=j )
{
solve.merge(i,j);
}
}
}
return solve.ret();
}
};- 改进之后
class UnionSet
{
public:
UnionSet(int n)
{
father.resize(n);
for(int i=0; i<n; ++i)
{
father[i]=i;
}
}
//修改merge的策略,稍微好一点
void merge(int first, int second)
{
int a=findFather( first );
int b=findFather( second );
if( a==b )
{
return ;
}
else
{
father[a]=b;
return ;
}
}
int ret()
{
int res=0;
for(int i=0; i<father.size(); ++i)
{
if( father[i]==i )
{
++res;
//cout<<"ok"<<i<<endl;
}
}
return res;
}
private:
vector<int> father;
int findFather(int val) //内部的辅助函数
{
while( val!=father[val] )
{
val=father[val];
}
return val;
}
};1.4.如何缩短findFather函数的搜索速度
- 显然,我们在每次查询findFather之后进行一次重新Father(val)=XXX就行了
- 我的想法是:只有findFather查询一次,我才优化一次『非必要不主动优化』
- 注意:我的方法和主流的UnionSet优化方式是不同的!!
2.单调栈MonotonousStack『模板』
参考:单调栈解题模板秒杀8个题
mo-not-on-ous
难点—不知道ADT
单调栈实际上是栈,只是利用一些巧妙的逻辑:
使得『每次』新元素入栈后,栈内的元素都保存单调!(单调递增或单调递减)
尝试创建:ADT
2.1.模板题
2.1.1.例1-最大的矩形
- CCF.2013 12-3.最大的矩形(单调栈)
2.1.2.例2-下一个更大的元素
2.1.3.每日温度
2.2.最终ADT模板设计✔️
- 这个栈满足一个性质:
- 这个算法的过程用一句话总结就是,如果压栈之后仍然可以保持单调性,那么直接压。否则先弹出栈的元素,直到压入之后可以保持单调性。
- 这个算法的原理用一句话总结就是,被弹出的元素都是大于当前元素的,并且由于栈是单调减的,因此在其之后小于其本身的最近的就是当前元素了
- 单调栈在栈的基础上进一步受限,即要求栈中的元素始终保持单调性。
//我们设计,从栈底到top是『单调递增』的
class MonotonousStack
{
public:
void push( int val );
int top( ); //返回栈顶
//push前调整栈的单调性『这个接口,本来不应该有的,但是很多单调栈的题目,很喜欢用这个二等公民』
void beginPushAdjust( int val );
private:
stack<int> data;
};- 实现如下
//我们设计,从栈底到top是『单调递增』的
class MonotonousStack
{
public:
void push( int val );
{
beginPushAdjust(val);
data.push(val);
}
int top( ); //返回栈顶
{
if( !data.empty() )
{
return data.top();
}
else
{
throw "error func call";
}
}
void beginPushAdjust( int val ) //push前调整栈的单调性
{
while( ( !data.empty() ) && data.top()>val )
{
data.pop();
}
}
private:
stack<int> data;
};2.3.单调栈解题『坑』『模板』⭐️
- 单调栈,用于解题,常常用的是『二等公民』
//伪代码如下
MonotonousStack solve;
for( 循环 )
{
solve.beginPushAdjust( 值val );
//获得solve.top();
//利用写你的解题逻辑
solve.push( 值val );
}3.单调队列MonotonousQueue『模板』可设计ADT
ACM中的使用:
单调队列:单调队列即保持队列中的元素单调递增(或递减)的这样一个队列『可以从两头删除, 只能从队尾插入』
- 这个队列满足一个性质:数列中的所有元素只会进出单调队列一次
3.1.模板题
3.1.1.例题-滑动最小值
- 《挑战程序设计竞赛》
3.1.2.志愿者选拔
3.1.3.滑动窗口的最大值
从front到队尾“单调递减”的单调队列的应用』
3.2.最终ADT模板设计✔️
- 从实际上还是队列,只是利用一些巧妙的逻辑:
- 使得『每次』新元素入队列后,队列内的元素都保存单调!(单调递增或单调递减)
- 这个队列满足一个性质:
- 单调队列在添加(push)元素的时候靠删除元素保持队列的单调性,相当于抽取出某个函数中单调递增(或递减)的部分。
- 设计的ADT的算法如下
- 设计从front到尾巴『单调递减的队列』
class MonotonousQueue
{
public:
//在队尾添加元素n,如果n比前面的元素大,则『压掉它』也就是去除
void push(int n);
//返回当前队列中的队头『单调递减,所以正好是队头』
int retFrontMax();
//队头元素如果刚刚好是val,那么删掉它!
void popIsVal(int val);
private:
deque<int> data;
};- //设计从front到尾巴『单调递增的队列』差不多同理
class MonotonousQueue
{
public:
//在队尾添加元素val,如果n比前面的元素大,则『压掉它』也就是去除
void push(int val);
{
//如果是非空的,并且data的尾巴元素小于val
while( (!data.empty()) && data.back()<val )
{
data.pop_back();
}
data.push_back( val );
}
//返回当前队列中的队头『单调递减,所以正好是队头』
int retFrontMax();
{
if( 0==data.size() )
{
throw "error func call";
}
else
{
return data.front();
}
}
//队头元素如果刚刚好是val,那么删掉它!
void popIsVal(int val);
{
if( ( !data.empty() && val==data.front() )
{
data.pop_front();
}
return ;
}
private:
deque<int> data;
};4.LRU题解的模版✅
- 1、用STL的list双向链表,精简代码
- 2、反思了一下,以前为什么C++设计的时候,迭代器有了end还要rbegin
- 3、这类设计数据结构的方式让我们思考C语言的严版的设计方式和我们C++面向对象的设计方式的异同
- C++设计数据结构,感觉就是推广了C语言数据结构的设计方式,思维方式就很想this指针如何用C语言实现一样
- 4、哈希的时候,那个key或者val,你可以展开思路!比如到迭代器!数组!数组套迭代器啥的!
//要使用unorder_map,它底层是散列,只会映射而不用排序,能够实现$O(1)$
//体现了STL中为什么,有end还要有rbegin的原因
//因为end指向的是指向最后一个元素的下一个节点,而rebgin体现的却是倒数第一个元素的位置
AC代码
get借助put精简代码的版本」迭代器的转换
✅记忆
std::next(it).base(); //反向迭代器转换为正向迭代器!class LRUCache {
private:
list< pair<int,int> > m_list; //key. val 不能仅val,因为我put的时候要删掉key的map
map<int, list< pair<int,int> >::iterator > m_mp; //key->iterator
int m_capacity;
public:
LRUCache(int capacity) :m_capacity(capacity){
}
int get(int key) {
if( m_mp.find(key) != m_mp.end() ){
int t_key=key, t_val= m_mp[key]->second ;
put( t_key, t_val ); //重新放进去,借助put精简代码
return t_val;
}
return -1;
}
void put(int key, int value) {
//如果存在原本的key,管你一样还是不一样
if( m_mp.find(key) != m_mp.end() ){
m_list.erase( m_mp[key] ); //清除list
m_mp.erase( m_mp.find(key) ); //清除map
}
//如果不存在、转换成的不存在
//去除「最久没访问的」
if( m_list.size()==m_capacity ){
//不是front是begin
list< pair<int,int> >::iterator it= m_list.begin();
m_mp.erase( m_mp.find( it->first ) );
m_list.pop_front();
}
//小的
//「坑点!反向迭代器和正向迭代器的转换!」
//std::next(it) 返回指向反向迭代器的下一个元素的迭代器,再通过 std::next(it).base() 将其转换为正向迭代器。
//注意,it 必须是 auto 类型,因为它的类型是一个反向迭代器,无法直接转换为正向迭代器
m_list.push_back( make_pair(key,value) );
auto it = m_list.rbegin();
//发现下面的转换结果是一样的
//cout<<"tempkey="<<it->first<<" val="<<it->second<<endl;
//cout<<"key="<<std::next(it).base()->first<<" val="<<std::next(it).base()->second<<endl;
m_mp[key]=std::next(it).base();
}
};
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache* obj = new LRUCache(capacity);
* int param_1 = obj->get(key);
* obj->put(key,value);
*/- 上面的,可以不使用迭代器转换,但是会超时22/22
auto it = m_list.begin();
int loop=m_list.size()-1;
//超时原因在这,但是没办法!因为it+=loop不行!it=it+loop也不行!
while( loop-- ){
it++;
}✅最终改善后的代码!我们把最久的放在list的末尾而不是首位-避免迭代器转换
class LRUCache {
private:
list< pair<int,int> > m_list; //key. val 不能仅val,因为我put的时候要删掉key的map
map<int, list< pair<int,int> >::iterator > m_mp; //key->iterator
int m_capacity;
public:
LRUCache(int capacity) :m_capacity(capacity){
}
int get(int key) {
if( m_mp.find(key) != m_mp.end() ){
int t_key=key, t_val= m_mp[key]->second ;
put( t_key, t_val ); //重新放进去
return t_val;
}
return -1;
}
void put(int key, int value) {
//如果存在
if( m_mp.find(key) != m_mp.end() ){
m_list.erase( m_mp[key] ); //清除list
m_mp.erase( m_mp.find(key) ); //清除map
}
//如果不存在+转换成的不存在
//比较大了
if( m_list.size()==m_capacity ){
//这里改了方向
auto it= m_list.rbegin(); //反向迭代器,但是这里没事!因为我后续只需要获得对应的元素
m_mp.erase( m_mp.find( it->first ) );
m_list.pop_back();
}
m_list.push_front( make_pair(key,value) );
auto it = m_list.begin(); //正向迭代器!
m_mp[key]=it;
}
};
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache* obj = new LRUCache(capacity);
* int param_1 = obj->get(key);
* obj->put(key,value);
*/面试问:正向迭代器和反向迭代器的区别
正向迭代器和反向迭代器都是用于迭代容器中元素的工具,但它们的方向不同。
正向迭代器是一种顺序遍历容器元素的迭代器,它按照容器中元素的顺序逐个迭代。例如,在一个列表中,正向迭代器将按照列表从左到右的顺序逐个迭代列表元素。
反向迭代器是一种逆序遍历容器元素的迭代器,它按照容器中元素的相反顺序逐个迭代。例如,在一个列表中,反向迭代器将按照列表从右到左的顺序逐个迭代列表元素。
在C++中,可以使用begin()和end()函数获取正向迭代器,使用rbegin()和rend()函数获取反向迭代器。
Trie-前缀树✅
前缀树,又称字典树,是 N 叉树的特殊形式。
Trie [traɪ] 读音和 try 相同,它的另一些名字有:字典树,前缀树,单词查找树等。
字典树类代码
class Trie
{
private:
//标记是否是单词结束
bool isEnd;
Trie* next[26];
public:
/** Initialize your data structure here. */
Trie()
{
isEnd = false;
memset(next, 0, sizeof(next));
}
/** Inserts a word into the trie. */
void insert(string word)
{
Trie* node = this;
for (char c : word)
{
if (node->next[c-'a'] == NULL)
{
node->next[c-'a'] = new Trie();
}
node = node->next[c-'a'];
}
node->isEnd = true;
}
/** Returns if the word is in the trie. */
bool search(string word)
{
Trie* node = this;
for (char c : word)
{
node = node->next[c - 'a'];
if (node == NULL)
{
return false;
}
}
//借助isEnd来看是不是最终的节点
return node->isEnd;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix)
{
Trie* node = this;
for (char c : prefix)
{
node = node->next[c-'a'];
if (node == NULL) {
return false;
}
}
//比如,apple的前缀可以是app,apple
return true;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
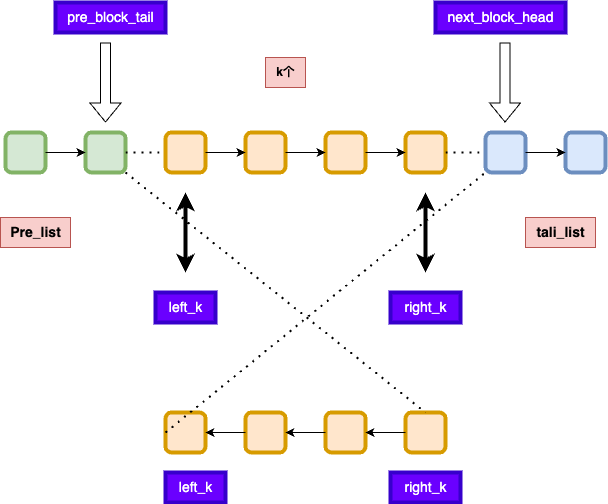
*/k个1组反转链表
- 个人模版:https://leetcode.cn/problems/reverse-nodes-in-k-group/
- 解体核心:
- 要有哨兵
- 要注意翻转后的位置
- 要注意k个一组,循环的时候是循环k-1次
- 解体核心:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverse( ListNode *head ){
ListNode * sentry=nullptr;
while( nullptr!=head ){
ListNode *temp=head->next;
head->next=sentry;
sentry=head;
head=temp;
}
return sentry;
}
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode* dummy=new ListNode( INT_MAX );
ListNode* preblock_tail=dummy;
ListNode* left_k=head;
ListNode* right_k=head; //初始位置
ListNode* nextblock_head=head; //暂时未知
//如果更新后的,后半部分链表不为空,我们尝试一下
while( nullptr!=nextblock_head ){
//move right, k-1
for(int i=1; i<k && nullptr!=right_k; ++i){
right_k=right_k->next;
}
//说明right和right不足k-1的距离,也就是【left,right】不足k个
if( nullptr==right_k ){
break;
}
nextblock_head=right_k->next;
right_k->next=nullptr; //截断和nextblock的连接
reverse( left_k );
preblock_tail->next=right_k;
left_k->next=nextblock_head;
//update data
preblock_tail=left_k;
left_k=nextblock_head;
right_k=nextblock_head;
}
ListNode* ret=dummy->next;
delete dummy;
return ret;
}
};